Research diversification benefits

The podcast episode “Richard Sutton - Father of RL thinks LLMs are a dead end” by Dwarkesh Patel discusses Richard Sutton’s critique of large language models (LLMs) and their limitations as a form of artificial intelligence. Here’s a detailed summary:

1. Introduction to the Topic:
   • Dwarkesh Patel interviews Richard Sutton, a pioneer in reinforcement learning (RL), who has recently expressed skepticism about LLMs and their potential for continual learning.
2. Sutton’s Perspective on RL vs. LLMs:
   • Sutton argues that understanding the world is the core problem of intelligence, whereas LLMs are primarily about mimicking human behavior by predicting what people would say in a given situation.
   • He asserts that true learning from experience involves not just repeating patterns but constructing an internal model to understand and adapt to one’s environment.
3. Critique of LLMs as “Dead Ends”:
   • Sutton claims that LLMs cannot learn on-the-job, or through direct interaction with the world, because they lack the ability to update their understanding based on new information. They are confined to predicting human responses rather than understanding the underlying dynamics of a situation.
   • He suggests that we’ll eventually need a new architecture for continual learning in AI, which could render current LLM approaches obsolete.
4. The Need for Goal-Directed Learning:
   • Sutton emphasizes that intelligence involves setting and achieving goals; without this ability to adapt strategies based on feedback from reality (not just historical patterns), an agent lacks the essence of intelligence.
   • He contrasts this with LLMs, which are expert predictors within a narrow domain but fail at broader generalization or pivoting to novel tasks.
5. Imitation Learning and Its Limitations:
   • The discussion touches on the concept of imitation learning in AI, particularly through large language models. Sutton argues that these models do not genuinely learn from experience but rather memorize patterns in human behavior, which he considers a different (and less sophisticated) form of learning than what animals and humans typically engage in.
6. The “Bitter Lesson” and Its Implications:
   • Sutton references his influential essay “The Bitter Lesson,” which posits that the key to scalable AI is continual learning from experience, not knowledge engineering or large pre-trained models. He suggests that while LLMs are powerful tools for specific tasks, they do not represent a breakthrough in AI’s ability to learn and adapt broadly, as envisioned by some proponents.
7. The Era of Experience vs. Current Paradigms:
   • Sutton envisions a future where AI learns continually from experience, similar to how humans develop knowledge and skills over time. This contrasts with current paradigms that rely on extensive pre-training followed by fine-tuning for specific tasks or domains.
8. Conversational Debate:
   • Throughout the conversation, there’s a lively back-and-forth between Sutton and Patel regarding definitions of learning, the nature of AI intelligence, and the capabilities of LLMs. They explore whether imitation learning in humans translates effectively to machine learning models and debate the necessity for goals in AI systems.

The podcast episode serves as a detailed exploration of Richard Sutton’s views on LLMs and their limitations, framed within the broader context of his ideas about how AI should learn and evolve—through goal-directed interaction with the environment rather than pattern recognition from vast datasets.

Morphisms: trajectory functors that map each time step to its corresponding sensory, action, or internal state, preserving the order.

Trajectory functors must satisfy conditions ensuring semantic continuity (e.g., local Markov property).

2.2 Semantic parsing function

Definition: A Yarncrawler is a functor from world-trajectory category to a category of semantic spaces equipped with:

• An assignment of “thread” objects for each sensory or action event.
• Trajectory-aware parsing functors that map sensorimotor traces to sequences of semantic threads, respecting trajectory annotations and internal state dynamics.

The Yarncrawler’s parsing function also includes a repair mechanism that updates the internal state and Markov blanket when entropy leaks or coherence breaks down, ensuring local viability (homeorhesis).

3. Homeorhetic Markov blanket maintenance

Definition: A Yarncrawler’s Markov blanket must satisfy the homeorhetic condition, which ensures that it adapts to maintain internal state coherence while allowing for entropic exchange with the environment:

For any sensory or active node , there exists a local entropy threshold such that:

If local entropy (e.g., surprise) at exceeds , then updates occur in the Markov blanket via thread re-stitching, preserving conditional independences and homeorhetic coherence.

4. Free energy minimization & RSVP integration

The Yarncrawler’s free energy principle can be formalized as:

Minimize surprise (i.e., expected entropy) across time while maintaining local viability bounds:

𝔼[∑_t H(X_t | E_t)] - β ∑_t C(S_t, A_t) ≤ F_0

where is a temperature-like parameter controlling the balance between surprise minimization and local coherence constraints (C), with being the initial free energy level.

This formulation integrates with RSVP by associating Φ (scalar coherence) with internal state viability, 𝒗 (vector flows) with active Markov blanket mediations, and S (entropy/negentropy balance) with homeorhetic adjustments to maintain local viability.

By formalizing the Yarncrawler as a trajectory-aware semantic parser within a world-trajectory category, this definition captures both its self-repairing nature and the homeorhetic Markov blanket maintenance essential for its operation. The free energy minimization principle further unifies surprise reduction with local viability constraints, providing a rigorous foundation for understanding how the Yarncrawler navigates high-dimensional input streams while maintaining semantic coherence.

The text presents a Yarncrawler framework, an abstract model for understanding how living systems parse their environments and adapt through self-repair. This framework is applied to both biological organisms (animals and plants) and theoretical models (like large language models - LLMs). It also extends this concept down to the molecular level using reaction-diffusion equations, membranes, selective channels/pumps, and autocatalysis.

1. Core Intuition: The Yarncrawler framework posits that living systems are self-repairing semantic crawlers. They don’t passively interpret their world but actively weave their own understanding by parsing inputs into meanings while recursively rewriting their internal lexicon of survival.

2. Markov Blanket Maintenance: The stabilizing structure is the Markov blanket, which separates self from the rest of the world. Unlike a static shell, this blanket is homeorhetic (trajectory-stabilizing). It consists of sensory nodes parsing environmental signals into provisional semantic attractors, active nodes weaving interventions back into the environment, and internal states storing and modifying recursive source code.

3. Semantic Parsing Function: Parsing in this context is trajectory-aware—inputs are not static tokens but threads with temporal arcs. Noise isn’t discarded; instead, it’s annotated for re-interpretation, allowing future repair. Each crawl or parse is a partial recompilation of the agent itself.

4. Self-Modification & Repair: Organisms identify tears (violations) in their blankets and patch them by re-threading semantic structure. Trajectory memory stores past repairs as scaffolds for future ones, enabling continual self-regeneration.

5. Theoretical Implications: The Yarncrawler framework formalizes active inference through minimizing surprise via repairing its interpretive grammar (Free Energy Principle). It also integrates with the RSVP interpretation, embodying local semantic attractors that maintain coherence, flow, and entropy within viable bounds. Critically, it argues that LLMs lack the yarncrawling capacity for continual self-repair, making them brittle parsers incapable of true general intelligence.

6. Formalization: The text proposes a category-theoretic interface (lax monoidal functor from world trajectories to semantic modules), sheaf semantics (local covers with non-unique global sections for ambiguity management), and the variational blanket principle (free energy minimization under consistency constraints). Repair is conceptualized as constrained rewriting, where patches are 2-cells in a reconfiguration category that preserves key invariants.

7. Comparative Analysis: The text contrasts yarncrawlers (animals and plants) with LLMs:

   • Caching & Deferred Use: Yarncrawlers cache using blurred gradients, not precise maps. Retrieval involves re-parsing cues rather than recalling coordinates. In contrast, LLMs operate on precompiled symbolic seams without adaptive repair.
   • Regeneration & Self-Repair: Yarncrawlers regrow limbs or rewire neural pathways when damaged. LLMs lack this capacity; they can only replay past contexts and don’t dynamically adapt their internal structure.
   • Tropism & Gradient Following: Yarncrawlers follow blurred probability fields, not explicit maps. LLMs operate on rigid prompts or token-level statistics, failing to adapt flexibly to new data streams.

8. Molecular Swarming as a Yarncrawler: The framework is scaled down to molecular swarms using diffusion, semi-permeable membranes, selective channels/pumps, and autocatalysis:

   • Diffusive Swarms as Proto-Crawlers: Molecules in solution move via Brownian diffusion, their dynamics constrained by a semi-permeable membrane. This setup maintains a scalar coherence (Φ), vector flows (𝒗), and entropy distribution (S).
   • Selective Ion Channels & Pumps = Active Parsing: Channels and pumps implement semantic parsing rules on molecular traffic, conditionally opening/closing or expending energy to drive flows against equilibrium. They maintain homeorhesis (flow-based stability) by repairing the system’s “blanket”.
   • Autocatalysis vs Collectively Autocatalytic Sets: Simple autocatalysis is fragile; collective autocatalysis robustifies the system by having multiple molecules catalyze each other’s production. This forms a Yarncrawler swarm, where coherence isn’t tied to one molecule but distributed across the network.
   • Emergent Behavior: Molecular Swarms as Parsers: A swarm of diffusing molecules with membrane selectivity and pumps, plus autocatalytic closure, functions like a molecular Yarncrawler—parsing gradients of chemical affordances instead of explicit maps. Noise provides diversity for autoc

The text provided appears to be a summary of various concepts from biophysics, chemical reaction networks, and systems biology, specifically focusing on the molecular-scale behavior of cells and their components. Here’s a detailed explanation of each section:

1. Pump Dynamics: This part discusses how ion pumps maintain cellular ion concentrations by consuming energy (ATP) to transport ions against their gradients. The formula provided describes the pump current for an active Na+/K+ ATPase-like pump, considering saturation kinetics and stoichiometric coupling. For secondary active transporters, the driving force is replaced with a gradient term like proton motive force. Homeorhesis refers to the maintenance of stable flows rather than static equilibria in cellular systems.

2. Reactions: This section distinguishes between autocatalysis (a single species catalyzing its own production) and collectively autocatalytic sets (RAF). The latter involves multiple reactions where each reaction is catalyzed by some molecule within a food set, creating redundant repair pathways that increase robustness against perturbations.

3. Gaussian-blur affordances: This concept describes how molecular swarms can follow smoothed opportunity fields instead of exact coordinates. A chemo-affordance potential (ψ) is obtained by applying Gaussian smoothing to heterogeneous sources, and the flux is augmented with a drift term that follows this blurred gradient.

4. RSVP mapping: This section introduces a set of functional definitions for a non-equilibrium system. Φ represents a scalar coherence/potential, combining interior free energy and imbalances to measure the overall system’s organization. v is the total flux field encompassing diffusion, drift, channel activity, and pump currents. S denotes entropy production or budget, which channels/pumps manage by exporting entropy while maintaining internal order.

5. “Yarncrawler” criteria: This checklist outlines essential properties for a cell’s molecular machinery to ensure viability at the single-cell level. These include maintaining separate conditions inside and outside (blanket maintenance), implementing traffic shaping through gating and pumping (active parsing), providing self-repair mechanisms through RAF networks, utilizing blurred gradients for navigation instead of exact maps (trajectory awareness), and maintaining stable flows (homeorhesis) that keep the system’s free energy bounded under sustained entropy export.

6. Minimal modeling recipe: This is a practical guideline for creating a simulation section focusing on molecular-scale cellular behavior. It suggests choosing species, defining their stoichiometry and catalytic coefficients to form a RAF, setting diffusion, chemotactic, and permeability coefficients, adding channels with gating ODEs, incorporating pumps with stoichiometry, and using split-step integration for reaction, diffusion, and boundary flux calculations. Key performance indicators should be monitored, such as blanket viability (ensuring ion concentrations remain within acceptable limits).

The provided LaTeX document presents the Yarncrawler Functor Master Equation (YFME), a unified field-theoretic formulation that integrates several biological processes. Here’s a summary and explanation of its key components:

1. Geometric & Physical Setup: The system is defined on an interior domain \(\Omega\) with boundary \(\Gamma\), modeled as a semi-permeable membrane (Markov blanket). Time \(t \in [0, T]\).

   • Bulk fields include species concentrations \(c_i(x,t)\), electric potential \(\varphi(x,t)\), and chemo-affordance potential \(\psi(x,t)\).
   • A semantic field is introduced through a gauge connection \(A_\mu\) on a bundle \(\mathcal{E}\), encoding parser modules with curvature \(F_{\mu\nu}\). Gauge repairs are local modifications to \(A_\mu\).
   • Boundary fields include permeabilities \(P_i\), channel gates \(\gamma_k(t)\), and pump flux intensities \(\Pi_a(t)\).

2. Action with Constraints (Onsager-Machlup + Gauge + Boundary Terms): The system is governed by a constrained variational principle over currents and fields. This yields diffusion, electrodiffusion, chemotaxis, reactions, and blanket fluxes as Euler-Lagrange conditions.

3. Euler-Lagrange Equations (YFME System):

   • Continuity: \(\partial_t c_i + \nabla\cdot \mathbf{J}_i = R_i(\mathbf{c})\), representing mass conservation of species \(i\).
   • Electrodiffusion: \(-\varepsilon \Delta \varphi = \sum_i z_i c_i\), modeling the electric potential and its relation to charged species.
   • Semantic gauge descent: Describes how the semantic field \(A_\mu\) evolves, balancing descent (driven by RSVP bookkeeping) with regularization terms.
   • Boundary flux law: Ensures that the total flux through the boundary equals passive permeation, channel-mediated transport, and pump activity.

4. RSVP Bookkeeping: Coherence \(\Phi_{\text{RSVP}}\) is defined as the negative free energy, providing a measure of system organization and viability.

5. Autocatalysis & RAF (Reaction Acceleration Factor): Reactions are represented by \(\dot{\mathbf{c}} = S\,\mathbf{v}(\mathbf{c})\), with reaction rates \(v_r(\mathbf{c})\) potentially boosted by the RAF mechanism.

6. Gaussian-Blur Affordances (Trajectory Awareness): The chemotactic term is generalized to incorporate trajectory awareness via convolution with a Gaussian kernel.

7. Rayleigh Dissipation & Master Equation Form: A quadratic dissipation potential is added for nonconservative processes, resulting in the Yarncrawler Functor Master Equation (YFME), which describes the damped, constrained evolution of the system.

In essence, this formulation captures various aspects of cellular biochemistry within a unified mathematical framework, enabling the study of complex behaviors such as self-repair, homeorhesis, and recovery from perturbations in noisy environments—aspects that distinguish it from single-loop autocatalyst models.

This LaTeX document presents several mathematical models, each associated with specific biological or physical phenomena. Here’s a detailed summary of each section:

1. Summation involving integrals: This part introduces an expression that appears to be an energy functional in the context of reaction-diffusion systems. It consists of two parts:

   • The first integral involves the product of concentrations (c_i) and their natural logarithms, which is weighted by coefficients (c_iref). This term might represent entropy production or free energy in thermodynamic contexts.
   • The second integral includes squared differences between input (ci^in) and output (ci^out) concentrations across a surface (denoted as Γ), possibly representing fluxes through a membrane.

   This functional is minimized or maximized, depending on the context, to find the equilibrium or optimal states of the system.

2. Autocatalysis vs. RAF: Here, we encounter reaction kinetics described by the Rate And Force (RAF) model, which extends classical autocatalytic models. The velocity vr(c) depends on concentrations (cm) and may include terms for cooperative effects through coefficients (αrm). This model allows for complex interactions between different species in a reaction network.

3. Gaussian-blur affordances: This section describes a process where an affordance (a potential action or interaction) is blurred using a Gaussian function G_σ. The output ψ results from convolving this Gaussian with some input u, and the resulting gradient (∇ψ) influences certain quantities χ_i ci. This could represent a smoothing or blurring of potential actions in a system, affecting the behavior of components based on concentrations ci.

4. Master equation form with dissipation: The fourth part introduces a more advanced model using the framework of stochastic thermodynamics. Here, an action principle (∂S/δq - d/dt(∂S/δ˙q) + ∂R/∂˙q = 0) is applied to describe dynamics under dissipation (R). This expression includes terms for the rate of change of a system’s state (∂t c), fluxes (J), reaction rates (R(c)), and Rayleigh dissipation quadratic in fluxes, time derivatives of certain quantities, pump currents, and diffusion coefficients. This formulation incorporates concepts like continuity constraints and blanket (or boundary) conditions, potentially used to model biological or chemical systems with detailed energy balance considerations.

5. 1D membrane-tube toy model: This subsection presents a simplified 1D reaction-diffusion-drift model within a tubular geometry. The system consists of one (or more) species c_i evolving according to reaction-diffusion dynamics inside a tube with fixed concentrations at both ends (ci,0out and ci,Lout). The key elements include:

   • Geometry & fields: A 1D tube [0, L] with reservoirs at each end having fixed c_i^out.
   • Bulk PDE: Reaction-diffusion-drift equation where the diffusion coefficient (D) and electrodiffusion factor (χ) govern the spatial spread of concentrations. An optional “Gaussian blur” term (ψ) can be included for affordance smoothing.
   • Reaction term (R(c)): This represents the local creation or consumption rates of species based on their current concentrations, encapsulating complex chemical interactions.
   • Membrane flux laws: Robin boundary conditions at x=0 and x=L, which dictate how species cross the membrane, influenced by passive leakage (κ) and active pumping (J_pump). The latter is linearized around an operating point for simplicity.

This toy model allows exploration of steady-state solutions and stability conditions under various parameters (diffusion rates, boundary fluxes, reaction kinetics), providing a simplified yet insightful framework to validate the more complex models described earlier before implementing lattice simulations.

This text presents a mathematical analysis of a system described by a partial differential equation (PDE) related to concentration dynamics within a domain from 0 to L, with certain boundary conditions and nonlinear terms. Here’s a detailed summary and explanation:

1. The PDE and its Steady State Solution: The main PDE is given by J(L) = -κ_L(c^out_L - c(L)) - π_L + α_Lc(L), where J, κ, c^out, π, and α represent specific parameters related to the system. The steady-state solution (where ∂tδc = 0) is given by two equations for c(x):

   c(x) = A + J when χΨ ≠ 0 (nonlinear drift case), or c(x) = Ae^(βx) + J when χΨ = 0 (no drift linear case).

   Here, A is determined by the boundary conditions and initial data.

2. Solving for Parameters: The system can be solved to find A and J* explicitly:

   For no drift (χΨ=0), we have the following closed-form solutions for A and J*:

   b = -J/D, J = [κ_0 κ_L (c^out_0 - c^out_L) + κ_0 π_L + κ_L π_0] / (κ_0 + κ_L + (κ_0 κ_L) L/D), a = c^out_0 - J*/κ_0

   Here, β is defined as χΨ/D, and D represents the diffusion coefficient.

3. Linear Stability Analysis: This section examines how small perturbations to the steady state grow or decay over time (linear stability analysis). We linearize the PDE around the steady-state solution c*(x) by assuming a normal mode form: δc(x,t) = e^(λt)u(x), where λ is the growth rate. This results in an ODE for u(x):

   Du’’ - χΨu’ + (R’(c) - λ)u = 0.

   The linearized boundary conditions are given by δJ(0) and δJ(L), which depend on the specific values of κ, α, c^out, and π at x=0 and x=L.

4. Reduction to Sturm-Liouville Problem: To simplify this ODE further, we apply a change of variables (u(x) = e^(βx/2)v(x)) that removes the first derivative term, reducing it to a standard Sturm-Liouville problem:

   v’’ + k^2v = 0, where k^2 = λ - R’(c) + D*β²/4.

The parameters κ, α, c^out, π, and χΨ represent physical properties of the system, such as diffusion coefficients, external concentrations, pump rates, etc., while A, J*, β, k, and λ describe characteristics of the steady-state solution and perturbation growth. The analysis provided helps understand how these parameters influence the system’s behavior, including its stability to small disturbances from equilibrium.

The provided text discusses several topics related to chemical reaction-diffusion systems with particular boundary conditions (BCs), stability analysis, and a comparison between single autocatalytic loops and collectively autocatalytic pairs. Here’s a detailed summary and explanation of the key points:

1. Wave Solutions and Robin Boundary Conditions:

   The given wave solution for a reaction-diffusion equation is: [ v(x) = A(kx) + B(kx) ]

   With Robin boundary conditions (BCs): [ x=0: -D(/2v(0)+v’(0))+,v(0)=-(_0+_0),v(0) ] [ x=L: -D(/2v(L)+v’(L))+,v(L)=(_L+_L),v(L) ]

   Using ( v(0)=A ) and ( v’(0)=Bk ), as well as ( v(L)=AkL+BkL ) and ( v’(L)=-AkkL + BkkL ), we obtain a 2x2 homogeneous system in terms of A and B. Nontrivial solutions require the determinant f(k) = 0, leading to eigenvalues λn = R’(c*) - Dkn^2 + ((χΨ)^2)/(4D).

   Stability Condition: Maxₙ Re⁡λn < 0 ensures stability. The least damped mode (smallest kn) determines the system’s behavior. A simple, usable test for stability is R’(c*) < Dk₁² - ((χΨ)^2)/(4D), with k₁ set by Robin leakage ((κ₀ + α₀), (κL + αL)). Larger leakage implies more stable behavior due to increased diffusion and blanket leakage.

2. Single Autocatalyst vs. Collectively Autocatalytic Pair:

   • Single loop (fragile): R(c) = ks c - δc ⇒ R’(c*) = ks - δ

   • Collective (2-species RAF, robust): ∂t c₁ = D₁ c₁’’ + a₁₁ c₁ + a₁₂ c₂, ∂t c₂ = D₂ c₂’’ + a₂₁ c₁ + a₂₂ c₂

     Linearized with the same Robin BCs. For spatial mode k, the Jacobian is: [ J(k) =

     \[\begin{pmatrix} a_{11}-D_1 k^2 & a_{12}\\a_{21}&a_{22}-D_2 k^2\end{pmatrix}\]

     ]

     Eigenvalues: λ±(k) = (trJ(k) ± sqrt((trJ(k))² - 4det J(k)))/2.

     RAF Advantage: Positive off-diagonal terms a₁₂, a₂₁ increase det J(k), lowering λ+(k) for the same diagonal gains—better stability margin under the same net growth. With blanket leakage, RAF pairs maintain viability where single loops blow up or collapse.

3. Optional Electrodiffusion (Ions, Constant-Field Approximation):

   The text briefly mentions electrodiffusion for ions ci with valence zi in a constant field. In the Goldman linearization, the transmembrane current at each end is approximately: [ J_{chan}^i g_i(- E_i), E_i = _T c_i ]

   This section seems to be an optional continuation discussing how ions’ electrodiffusion can affect the system’s behavior, likely in the context of reaction-diffusion equations involving charged species. The detailed explanation is not provided in the given text.

The provided text is a detailed description and mathematical representation of the Yarncrawler model, which is a theoretical framework used to understand how systems maintain coherence or stability while interacting with their environment. This model is inspired by biological systems and can be applied across various domains like molecular swarms, plants, animals, and even artificial agents such as language models (LLMs) or robots.

1. Mathematical Representation: The core of the Yarncrawler model involves several equations:

   • Current-Nernst Equation: Describes the flux (J_i^chan) of a species i across a channel, which is approximately equal to the conductance (g_i) times the difference between the applied potential (Δφ) and the Nernst potential (E_i). The Nernst potential (E_i) is calculated as the product of the thermal voltage (φ_T), natural logarithm, and the ratio of the species concentrations outside to inside the system (c_i^out/c_iin).

   • Total Current Neutrality: At steady state, the sum of the products of the charge (z_i) and flux (J_i) for all species is zero. This leads to an equation for the adjusted potential difference (Δφ*) that balances the Nernst potentials weighted by their conductances.

2. Biological Interpretations: The model’s components are mapped onto biological systems:

   • Ball of string through a straw (Molecular swarms): Here, the ‘ball of string’ represents hidden states or internal dynamics; the ‘straw’ is the Markov blanket, acting as a semi-permeable interface; the ‘spray’ is like reinforcement updates or active inference, preventing system unraveling; and rewrapping is analogous to semantic repair.

   • Self-knitting sock (Plants): In this metaphor, each stitch represents a local parsing decision in plant growth; the cuff symbolizes the boundary condition where new tissues must hold integrity; dropped stitches are like tears needing repair; and the continuous knitting illustrates homeorhesis—stability through flow rather than static equilibrium.

   • Train with repair engine (Animals): The ‘engine’ corresponds to self-repair processes, ‘cars’ represent functional modules or policies, and the ‘track’ signifies environmental cues or affordances. As the train moves, it simultaneously repairs itself and its track, maintaining motion continuity—akin to how animals couple movement with homeostasis and repair.

3. Artificial Agents (LLMs and robots): The text also introduces a comparison between natural Yarncrawlers and artificial ones:

   • While biological systems have intrinsic, self-maintaining Markov blankets (like semi-permeable membranes or tissue boundaries), artificial agents typically rely on externally imposed interfaces such as input/output channels, token streams, or human curation.

   • The coherence (\(\Phi\)) in artificial systems is a property of the stability of high-dimensional manifolds (like language model embeddings) rather than being sustained by endogenous repair mechanisms. Flows (\(\mathbf{v}\)) are token sequences across trajectories, pre-shaped by training data instead of adaptive environmental interactions. Entropy (\(S\)) in artificial systems may manifest as hallucinations, error cascades, or distributional drift, unlike the entropy export in biological systems through processes like metabolism and senescence.

The critique is that artificial Yarncrawlers lack the robust homeorhetic repair dynamics seen in natural systems, forming coherence in a potentially thinner, more fragile manner due to their reliance on complex manifolds rather than intrinsic self-repair mechanisms.

This toy model presents a “semantic transition compiler” for an artificial thick Yarncrawler, aiming to patch its own generative law (transition model) in response to detected “tears” or discrepancies. Here’s a detailed explanation of each step:

1. Base setup (latent dynamics + blanket):

   The internal state x_t evolves under a parametric transition model p_θ(x_{t+1} | x_t, a_t) and observation model p_θ(y_t | x_t). This evolution is governed by an exponential-family parametrization, where natural parameters η_θ(x,a) and sufficient statistics T(x’) relate to the transition probabilities. A Markov blanket (S for sensors and A for actuators) controls data flow into and out of the system.

2. Tear detector (find “leaky” locales):

   To detect discrepancies in the model, a prediction residual r_t is calculated as the difference between the true sufficient statistics T(x_{t+1}) and the expected values under the current parameterization θ. The tear score Δ_U quantifies the total squared error within a window U: Δ_U = (1/|U|) ∑_t∈U ||r_t||^2_2.

   If this score exceeds a threshold τ, and the blanket factorization holds (all updates pass through S and A), a patch is triggered to repair the tear.

3. Local patch (compiler step):

   The local repair involves introducing a locale-selector P_U that activates only within the detected window U. This selector, along with a regularization term λ∥δ∥_1 for sparsity and MDL principles, defines a constrained optimization problem:

   minimize δ_U * such that F_U(θ + P_U δ) + λ ∥δ∥_1 + γ ∑_V∈N(U) ||G_U δ - G_V δ||_2^2

   Here, F_U represents the local free energy (negative evidence bound), and G_U/G_V are coupling terms enforcing consistency across neighboring locales V ∈ N(U). The optimization problem ensures that updates stay within a valid parameter manifold via a projection operator Π_valid.

   After finding the optimal patch δ_U *, it is compiled into the system’s parameters: θ ← Π_valid (θ + P_U δ_U *).

4. “Pump” counter-term (online control during repair):

   While estimating the patch, a counter-flux (analogous to a membrane pump) is injected into the system to prevent drift. This ensures that the system remains stable while undergoing repairs, mimicking how biological systems maintain internal equilibrium despite ongoing self-maintenance processes.

This model provides an explicit mathematical framework for an artificial thick Yarncrawler’s self-repair capabilities. It demonstrates how such a system could detect discrepancies (tears), compile localized patches while enforcing consistency and sparsity, and maintain stability during the repair process—all key aspects of natural thick Yarncrawlers like plants and animals.

In the cultural evolution interpretation of the Yarncrawler framework, two key processes—stigmergic path clearance and berm creation—are used to represent membrane and Markov blanket functionalities. Here’s a detailed explanation:

1. Stigmergy as Blanket Maintenance:
   • In this context, stigmergy refers to the indirect communication through environmental modifications, like insects clearing trails or humans building berms. These actions serve as external cues that regulate the flow of bodies and goods, akin to ion channels regulating molecular flux.
   • Membrane analogue: The path serves as a boundary separating what is considered “inside” (viable cultural niche) from “outside,” similar to how membranes separate cellular systems in biology. Landmarks act as reference points closing loops of expectation, much like Markov blankets in defining the system’s boundaries by considering statistical dependencies.
   • Cultural agents, through leaving traces (paths or berms), are essentially parsing their environment and modifying their parsing rules. The path “teaches” walkers how to follow it; a well-defined berm “teaches” builders how to maintain boundary boundaries.
2. Path Clearance = Entropic Export:
   • Path clearance can be seen as an entropic export process, where disorder (entropy) is removed and redistributed elsewhere (side piles or surrounding areas). By clearing paths, agents reduce the disorder or uncertainty in navigation, thus increasing coherence within the cultural system.
   • Free-energy expenditure: The labor or time invested in path clearance is analogous to the free energy spent in maintaining low-entropy states against thermal noise (in biological systems). This investment pays off by enhancing legibility and affordances, making traversals easier and more efficient.
   • Well-worn cultural trails persist because they represent low-entropy attractors; each traversal reaffirms the trail’s utility, reinforcing its role in reducing traversal entropy and increasing coherence within the system.
3. Berm Creation = Selective Permeability:
   • Berms or boundary markers function as semi-permeable membranes, controlling the flow of resources, ideas, or individuals across boundaries. They create a selective permeability that influences what information or entities cross the boundary.
   • In this context, berms help shape the Markov blanket by defining which variables (cultural elements) are relevant within a niche and which can be considered external. By doing so, they maintain the statistical dependencies necessary for defining the system’s boundaries while allowing controlled exchange with the broader environment.

This cultural evolution interpretation extends the original Yarncrawler framework to explain how collective behaviors (path clearance and berm creation) contribute to maintaining system boundaries, regulating information flows, and enhancing overall coherence in sociocultural systems—much like membranes and Markov blankets do in biological active inference.

State Variables:

1. C_offal (t) - Total mass of organic waste (food scraps, dung, offal) deposited at the berm, measured in kg.
   • Reaction: Decomposition by microorganisms to produce humics and nutrients.
2. C_ash (t) - Accumulated ash from cooking/heating fires, in kg.
   • Reaction: Buffering effect on soil pH through the release of cations (K, Mg).
3. C_char (t) - Mass of charcoal (biochar) added to the berm, in kg.
   • Reaction: Sorption of nutrients and microbial colonization.
4. C_shells (t) - Total mass of shell fragments added, measured in kg.
   • Reactions: Carbonate buffering and phosphorus input through mineral dissolution.
5. C_humics (t) - Concentration of humic/fulvic acids produced from decomposition, dimensionless [0,1].
   • Reaction: Formation from waste decomposition, catalyzed by charcoal pores and microbial activity.
6. C_buffers (t) - Total mass of buffering salts (carbonates, phosphates) in the berm, kg.
   • Reactions: Neutralization of acids through shell dissolution and charcoal interactions.
7. C_stable (t) - Mass of stable organic-mineral complexes formed in the berm’s structure, kg.
   • Reaction: Aggregation of humics with mineral particles and stabilized by charcoal.
8. C_worms (t) - Population density of earthworms in the berm, dimensionless [0,1].
   • Reaction: Enhanced mixing and aggregation via worm casts.
9. C_microbes (t) - Total biomass of microorganisms in the berm, kg.
   • Reactions: Catalyze decomposition, nutrient cycling, and formation of stable organic complexes.
10. C_roots (t) - Mass of plant roots entering the berm ecosystem, kg.
    • Reaction: Increased litter input fuels microbial activity and contributes to soil structure.

Reactions:

• Waste decomposition:

  dC_offal/dt = -k1*C_offal  // Decomposition rate constant k1
  dC_humics/dt = k1*C_offal * f_decomp(C_char, C_buffers) // Humic formation function f_decomp

• Sorption and humification:

  dC_char/dt = k2*C_offal * f_sorb(C_humics)  // Charcoal enhancement of sorption, rate constant k2
  dC_stable/dt = k3*C_humics * C_microbes * f_humify()  // Humification, rate constant k3

• Buffering:

  dC_buffers/dt = -k4*C_shells + k5*C_ash  // Carbonate production from shell dissolution and release from ash, rate constants k4, k5

• Worm colonization:

  dC_worms/dt = k6*C_stable * f_colonize()  // Worm attraction to stable organics, rate constant k6

Catalytic Boosts:

• Charcoal enhances decomposition by hosting microbes and adsorbing nutrients.
• Microbial exudates increase charcoal surface area for sorption.
• Worm casts provide new habitats for microbes, speeding decomposition and aggregation.

Parameters:

• f_decomp(C_char, C_buffers) - Function representing how charcoal and buffers affect humic formation rates (0 to 1).
• f_sorb(C_humics) - Function describing sorption enhancement by humics (0 to 1).
• f_humify() - Function modeling the efficiency of microbial humification (0 to 1).
• f_colonize() - Function indicating how stable organic matter attracts earthworms (0 to 1).

Bifurcation Analysis:

• Threshold for self-sustaining berm: As charcoal addition and decomposition rates increase, the system shifts from non-persistent (waste loss dominates) to persistent (berm growth exceeds losses). This transition depends on parameter values like k1, k2, k3, and initial conditions.

What to Measure:

• Berm biomass (sum of stable organics, humics, and microbial biomass).
• Soil structure metrics like aggregation stability or porosity.
• Microbial community composition/diversity as an indicator of ecosystem health.
• Nutrient availability and plant growth metrics to assess fertility enhancement.

This text presents a comprehensive model for soil dynamics, focusing on the interplay between biochar (black carbon), nutrients, microbial biomass, stable organic matter, buffer capacity, and soil structure within a spatial context. The model is divided into two main parts: Ordinary Differential Equations (ODE) for a single berm and Partial Differential Equations (PDE) for a spatial berm network.

1. ODE Model:

The ODE model describes the dynamics of six key components within a single berm, represented by variables: C (biochar), N (nutrients), B (microbial biomass), H (stable organic matter), S (buffer capacity), and M (soil structure).

• Biochar Input: u_C(t) represents the daily input of biochar into the berm, with a slow loss rate k_C.

• Nutrient Input: u_N(t) denotes nutrient input through dung/offal and shells/ash/buffer, with a balance maintained by microbial uptake ρ_B(NK/KN+N)B, leaching ℓ_N(N/(1+α_CC+α_HH)), and humification y_Hμ_Bϕ_p(S)(NK/KN+N)B.

• Microbial Biomass: Biotic growth is modeled by μ_Bϕ_p(S)(NK/KN+N)B, with turnover rate d_B.

• Stable Organics (Humus): Humification occurs at a yield y_Hμ_Bϕ_p(S)(NK/KN+N)B, and accrual is slowed by decay rate d_H.

• Buffer Capacity: Sorption and retention of nutrients by biochar (C) and humics (H) are represented, with buffer input u_S(t), dissolution rate k_S, and pH-dependent boost ϕ_p(S).

• Soil Structure: Aggregation builds structure via biota and char/humic catalysis γ_Mψ(C,H)B/(B+KB)(1-M), with erosion/fragmentation rate δ_Mχ(rain)M.

2. PDE Model (Spatial Berm Network):

The PDE extension accounts for spatial effects and overland runoff in a two-dimensional landscape (Ω ⊂ R^2). The equations are similar to the ODE model, but with diffusion terms (D_C, D_S, D_N, D_B, D_H) for organics and biota, advection of nutrients in runoff, and stigmergic deposition at boundaries.

3. Nonlinearities and Modulators:

• Buffering Effect: Sorption/retention is enhanced by ψ(C, H), which increases with biochar (C) and humics (H).

• pH Dependence: Biotic rates are modulated by pH-dependent factor ϕ_p(S).

• Rain Impact: Erosion/fragmentation is influenced by rain intensity, χ(rain), which can be storm-inducing (>1) or less intense (0.5-1 during dry spells).

This model captures the feedback loops and complex interdependencies within soil ecosystems, allowing for a deeper understanding of how different components interact and evolve over time. It provides insights into how biochar inputs can influence nutrient dynamics, microbial activity, and soil structure, ultimately affecting overall ecosystem health and productivity.

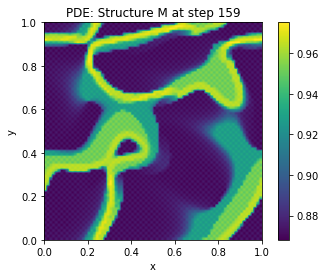
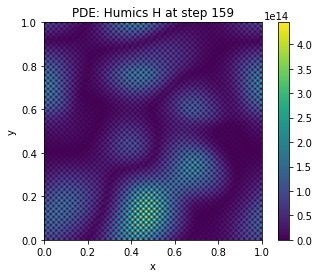
The provided text appears to be a description of a complex ecosystem model, likely for simulating the growth and dynamics of biofilms or similar structures on berm edges (e.g., raised pathways or barriers). The model incorporates several components: Organic matter (C), Humus (H), Biomass (B), Settlements (N), and possibly others, each with their own dynamics governed by a set of Ordinary Differential Equations (ODEs) and Partial Differential Equations (PDEs).

Here’s a detailed breakdown:

1. Variables:

   • C: Organic matter concentration.
   • H: Humus concentration, which accumulates as organic matter decomposes.
   • B: Biomass (biofilm) concentration, representing the living material on the berm edges.
   • N: Settlements, presumably representing entities like microorganisms or other biotic components that influence the system.

2. Governing Equations: Each variable has an associated ODE that describes its rate of change over time due to various processes:

   • C evolves based on production from nutrient inputs, loss through leaching, and conversion to humus by biomass.
   • H accumulates as a result of biomass-driven humification and decays over time.
   • B grows via effective birth (a function of humic concentration, nutrient flux, and a viability threshold), decays, and also influences humus accumulation and biomass aggregation.
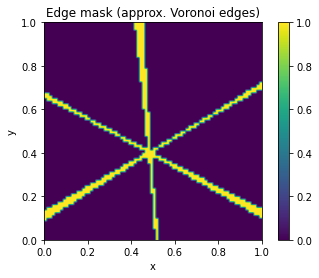
   • N is affected by settlement deposition, losses due to runoff and aggregation, and potentially other factors like birth/death processes or interactions with the environment.

3. Boundary and Forcing Conditions: The model includes a Voronoi-like pattern of berm edges, determined by the nearest settlement points. Deposition to these edges is influenced by visibility (a function of humus, biomass, and possibly other factors) and stigmergic gains (feedback effects enhancing edge maintenance).

4. Thresholds, Stability, and Diagnostics:

   • Viability Threshold: A condition for persistent biota (B growth), which involves a balance between effective birth rates and decay.
   • Coherence Score (Φ): A metric to assess system stability, with weights for different components and minimum thresholds to ensure the model doesn’t degrade into uncontrolled eutrophication or other chaotic states.
   • Logging and Monitoring: Suggested metrics include berm thickening times, humus growth rates, nutrient retention fractions, and response to perturbations (RAF fingerprint).

5. Minimal Parameter Sketch: A set of dimensionless parameters is provided for growth/decay rates, retention efficiency, buffering capacity, aggregation dynamics, and input means. These are illustrative and can be adjusted based on empirical data or specific research goals.

6. Stigmergy and Visibility: The model incorporates stigmergic behavior (local actions influencing the environment) through a visibility function that modifies deposition rates based on humus, biomass, and possibly other factors. This encourages edge maintenance in areas of high traffic or biomass concentration, potentially leading to a Voronoi-like pattern of thicker berm edges.

In summary, this ecosystem model simulates the dynamic interactions between organic matter, humus, biomass, and settlements on berm edges, using a combination of ODEs and PDEs. It incorporates stigmergic behaviors to mimic self-organizing patterns and includes stability diagnostics to ensure the system doesn’t devolve into uncontrolled states. The model is designed to explore how these components interact over time under various conditions, with applications in environmental science, ecology, or bioengineering contexts involving biofilm dynamics on man-made structures.

This theoretical interpretation of an “Ideal Yarncrawler” is a conceptual framework that connects the observed behaviors in squirrel caching, berm-building, and the proposed Yarncrawler system to fundamental ideas in machine learning (Mixture-of-Experts - MoE), information theory (Retrieval-Augmented Generation - RAG), and differential geometry (Semantic Field Trajectory Engine). Here’s a detailed explanation:

1. Mixture-of-Experts (MoE) as Cultural Weaving: In the context of Yarncrawler, each “expert” represents a cached affordance cluster or a squirrel’s nut cache. These experts are essentially local submodels within a larger system that specializes in handling specific types of information or tasks. The routing layer, or stigmergic attention field, determines which expert gets selected based on usage frequency (i.e., thickened by repeated use). This creates redundancy and resilience because even if one expert/cache fails, the system can still function due to the existence of other experts.

2. Retrieval-Augmented Generation (RAG) as Stigmergic Repair: RAG is more than just a combination of retrieval and generation; it’s a continuous loop that maintains an external memory store. In Yarncrawler terms, this can be likened to the process of caching semantic material and then re-retrieving and re-caching it back into the world—much like how cairns are built or berms are thickened over time. This RAG mechanism ensures that the cultural “blanket” remains robust by increasing redundancy in markers, i.e., cached information.

3. Complex Manifold = Semantic Field Trajectory Engine: Here, each expert (cache, berm, submodel) is considered a local chart on a semantic manifold. Retrieval serves as the transition function between these charts. The routing/attention mechanism ensures coherence or geodesic consistency when moving across different charts. Over time, the Yarncrawler’s path through this manifold forms a trajectory engine—not just representing states but actively shaping future paths by maintaining semantic coherence.

4. RSVP Interpretation:

   • Φ (coherence): Represents the global structure of the semantic field, ensuring consistent meaning survives perturbations.
   • 𝒗 (flows): Describes the dynamics across local charts, guided by stigmergic cues like cache density or berm visibility.
   • S (entropy): Measures the accumulated uncertainty/noise in seams, managed via retrieval and repair mechanisms (RAG, autocatalysis).

In essence, this “Ideal Yarncrawler” is a self-maintaining system that evolves to form a semantic manifold with RAG-mediated transition maps. It’s not just static knowledge storage; it actively generates meaning through continuous self-repair and trajectory navigation in the semantic field. This interpretation leverages concepts from category theory (experts as endofunctors), differential geometry (semantic manifold), and information theory (RAG, entropy management) to provide a unifying framework for understanding complex cultural evolution dynamics.

This text describes a complex system that combines concepts from differential geometry, machine learning, and information retrieval to form an advanced model for tasks involving spatial data with local knowledge. Let’s break it down into parts:

1. Manifold with Atlases and Local Parametric Fields:

   • The system operates on a manifold M (a generalization of the concept of a curve or surface to higher dimensions), which is divided into charts {(Ui, φi)}i∈I. Each chart Ui is an open set in M, and φi: Ui → ℂ^di (or ℝ^di) is a homeomorphism (a continuous function with a continuous inverse).

   • On each chart, there’s a local parametric field Ei: (φi(x), ξ) ⟼ (fi(φi(x), ξ), Ai(φi(x), ξ)). Here, fi is a vector field or policy/dynamics, and Ai is a local semantic potential or repair field. ξ represents retrieved facts.

2. External Memory (RAG):

   • The system uses an external memory K = {km} with an embedding ϕ: W ∪ M → ℝ^p, where W is the set of possible inputs and M is the manifold.

   • For a query q, retrieval kernel R(q) calculates similarity scores ωm(q) for each fact km in the memory using exponential functions based on cosine similarity between embeddings. The result is a weighted sum of facts from K.

3. Routing and Gluing (Partition of Unity + Sheaf):

   • Smooth, nonnegative functions αi: M → [0, 1] are defined with support ⊂ Ui, such that ∑i αi(x) = 1 for all x in M. These are known as a partition of unity.

   • Using the partition of unity, we can define global vector fields F(x, ξ) = ∑i αi(x) fi(φi(x), ξ) and global potentials A(x, ξ) = ∑i αi(x) Ai(φi(x), ξ).

   • Semantic presheaf/sections are introduced to ensure local consistency. For an open set V ⊂ M, S(V) is the space of admissible local parses/policies on V. Restrictions ρUV: S(V) → S(U) ensure compatibility when moving from larger to smaller sets U ⊂ V. A global section s ∈ S(M) exists if its local counterparts si ∈ S(Ui) agree on overlaps (seam loss).

4. Seam Loss:

   • Seam loss Lseam is a penalty term used to ensure continuity across chart boundaries. It’s defined as the sum of squared differences between fi and gij^(-1) fj, integrated over overlapping regions Ui ∩ Uj with weight wij(x), normalized by μ(x).

5. RAG as Transition Correction (Čech Coboundary Update):

   • A correction Δij(x; ξ) is computed based on retrieved facts ξ using the RAG, approximated via an optimization problem that minimizes discrepancies between fi and gij^(-1) fj + Δ. This correction can be viewed as a Čech coboundary update in sheaf theory, adjusting local field behaviors to ensure consistency across chart boundaries.

In essence, this system combines manifold geometry with machine learning concepts (like parametric fields and partition of unity) and information retrieval techniques (using RAG for external memory). It aims to create consistent, globally valid models from locally defined components while maintaining flexibility and adaptability through the use of a partition of unity and RAG-based corrections. This makes it suitable for tasks involving spatial data or geometric structures where local knowledge is available but global consistency is required.

The provided text outlines a complex system that combines several concepts from machine learning, control theory, and differential geometry to create an advanced model for decision-making and information processing. Here’s a detailed breakdown of each section:

1. Update Transitions: This introduces new transition functions for states g_ij~ and outputs f_j~. The update is based on exponential transformations of the original functions, weighted by some scalar Δ_ij, designed to improve overlap consistency across different patches or regions.

   • \tilde g_{ij} = \exp(\Delta_{ij})\circ g_{ij}: This updates the transition function g_ij by applying an exponential transformation and then composing it with the original function.
   • f_j~ = f_j \circ \exp(-\Delta_{ij}): This updates the output function f_j by applying an exponential transformation in reverse, followed by composition with the original function.

2. Seam Loss: The seam loss \mathcal{L}_{\text{seam}} is introduced to ensure consistency across overlapping regions or patches. It drives the system’s behavior (↓ L_seam ↓) and encourages retrieval of context that maintains overlap consistency rather than focusing solely on local weights.

3. Trajectory Engine (Controlled ODE/Differential Inclusion): This section defines a dynamical system for controlling actions u_t in response to retrieved context \xi_t. The dynamics are given by an ordinary differential equation (ODE), which can be formulated as a differential inclusion if the gates (expert functions) are sparse or hard.

   • x˙_t = F(x_t, ξ_t) + B(x_t)u_t: This is the general ODE describing the system’s evolution over time, where F encodes task-specific dynamics and B relates control inputs to changes in state.
   • If gates are sparse/hard: x˙_t ∈ co{f_i(φ_i(x_t), ξ_t) : α_i(x_t)>0} + B(x_t)u_t: Here, the system’s dynamics are defined over the convex hull of active expert functions.

4. Objective/Viability: The goal is to find optimal control inputs u_1:T* that minimize an expected cost over a time horizon [0, T]. This cost includes task performance (ℓ(x_t)), seam consistency (βL_seam(x_t, ξ_t)), and coherence gain (-γ∂Φ(x_t)/∂t), subject to viability constraints (x_t ∈ C).

5. Markov Blanket & Free Energy (RSVP): This introduces a probabilistic graphical model with internal states X_t, externals E_t, blanket nodes S_t, A_t (divided into sensory and active components), and assumes a blanket factorization. Variational free energy is defined over a local horizon Δ.

   • Ft: t+Δ = E_q_ϕ[log q_ϕ(X, S) - log p_θ(E, X, S|A)]: This defines the variational free energy functional over time.
   • RSVP (Recognition, Sensory, Valuation, Plan) maps are defined to compute the negation of free energy (Φ(x) = -Ft), the valuation function (v(x) = Ft(x, ξ)), and the entropy budget (S = ∫σ(x)dt).

6. Gauge View (Semantic Repair as YM Descent): This introduces a semantic connection A with curvature FA, penalizing roughness and seam curvature through an energy functional J[A, {fi}]. The repair flow is described by gradient descent on this functional.

   • J[A, {fi}] = ∫_M (1/2g^2 ||FA||^2 + η||∇AF||^2 + βL_seam)dμ: This defines the energy functional for semantic connection repair.
   • Repair flow: \partial_\tau A = -δJ/δA, \partial_\tau fi = -δJ/δfi: This describes how the semantic connection and expert functions evolve over time to minimize the energy.

7. Two Basic Results (Sketches): Two propositions are presented as sketches:

   • Proposition 1 states that under certain conditions on smoothness and partition of unity, a Mixture-of-Experts (MoE) model can approximate a continuous global field uniquely up to a gauge transformation.
   • Proposition 2 asserts that the Retrieval-Augmented-Graph (RAG) gluing process converges geometrically in expected seam loss under specified conditions on Lipschitz continuity and retrieval kernel properties.

8. Ideal Yarncrawler = MoE + RAG Master Equation: This section combines the dynamics, repair flow, and blanket maintenance into a unified framework for decision-making and information processing:

   • x˙_t = F(x_t, ξ_t) + B(x_t)u_t: This equation describes how the system evolves over time, integrating task dynamics (F), control effects (B with inputs u_t), and retrieved context (ξ_t).

In summary, this model combines ideas from mixture-of-experts architectures, differential geometry, and control theory to create a sophisticated framework for decision-making under uncertainty. It emphasizes maintaining consistency across overlapping regions, incorporating external context, and adapting through learning. The model’s dynamics are governed by a master equation that integrates task performance, seam consistency, coherence gain, and control inputs, all subject to viability constraints.

The provided text presents a formal mathematical model of an “Ideal Yarncrawler” across three scales—ecological, cultural, and artificial—each tied to the Relativistic Scalar Vector Plenum (RSVP) field theory. This idealized system is described as a self-refactoring semantic field engine that navigates inputs, repairs its structure, and accumulates knowledge through stigmergic reinforcement.

1. Ecological Yarncrawler (Squirrel Foraging & Gaussian Affordances):

   • Affordance Field: The squirrel perceives a smoothed distribution of resources (seeds, cover sites) denoted by the function ψ(x). This perceived affordance field is derived from an underlying resource distribution u(x) convolved with a Gaussian kernel Gσ. The equation is:

     ψ(x) = (G_σ * u)(x) = ∫ G_σ(x - y) u(y) dy

   • Foraging Dynamics: The squirrel’s movement is governed by the gradient of this perceived affordance field, adjusted for exploratory noise η(t):

     ẋ(t) = -∇ψ(x) + η(t)

   • Cache Reinforcement: Whenever a squirrel caches resources at location x, the local resource density u(x) is increased by a small amount δ:

     u(x^*) ↦ u(x^*) + δ

2. Cultural Yarncrawler (Berms, Cairns, Terra Preta):

   • RAF-style Growth Law: The cultural offloading system follows a reaction-diffusion-advection (RAF) style growth law for berm biomass/structure M(t), humics H(t), and biota B(t). The equations are:

     Ẁ = αHB - λM + κI(t)
     Ĥ = βf(offal, shells, dung) - μH
     Ḃ = γH(1 - B/Bmax) - νB

   • Stigmergic Input Rate: The input rate I(t), representing the salience of the berm, is influenced by the berm biomass M and adheres to a threshold Mcrit:

     I(t) = I_0 + ρσ(M - Mcrit)

In this model, the Gaussian kernel Gσ captures the squirrel’s perceptual noise, while the stigmergic input rate I(t) reflects how cultural artifacts (like berms or cairns) become more prominent as they accumulate and contribute to their maintenance. The RAF-style growth law for the cultural system shows how biomass, humics, and biota interact through reaction (αHB), diffusion (-λM), advection (κI(t)), production (βf), decay (-μH), and saturation (γH(1 - B/Bmax)) processes.

This mathematical formalization allows the ecological, cultural, and artificial Yarncrawler processes to be treated within a unified framework grounded in RSVP field theory, providing a common language for understanding and comparing these seemingly disparate phenomena.

The provided text outlines a conceptual framework for a “Yarncrawler,” which is a complex system inspired by various natural phenomena like squirrel caching behavior, berm formation, and microbial processes. It’s presented as a combination of several interconnected models, primarily leveraging ideas from stochastic processes, geometric tessellation, machine learning (specifically Mixture-of-Experts models and Retrieval-Augmented Generation), and information theory.

1. Squirrel Caching & Berm Formation:

   This part describes a model where ‘berms’ (accumulated material) form at Voronoi edges in a similar manner to how squirrels might cache food. The berm mass accumulates until it exceeds a critical threshold, after which the accumulation rate accelerates. This behavior is represented mathematically using a sigmoid function and geometric tessellation.

2. Mixture-of-Experts (MoE) with Retrieval-Augmented Generation (RAG) as Semantic Field Engine:

   Here, the authors propose a semantic field engine that integrates MoE and RAG models. This system is structured around local experts, each defining a scalar potential in its domain of expertise, which are then glued together by gating functions forming a partition of unity. The resultant global scalar field represents a coherent semantic manifold.

   • Expert Fields: Each expert Ei defines a local scalar potential φi(x).
   • Gating Functions: These (wi(x)) sum to one, ensuring they form a partition of unity.
   • Global Scalar Field: Φ(x) = ∑i wi(x)φi(x).
   • Semantic Vector Flow: v(x) = -∇Φ(x), indicating the direction and speed at which semantic information flows.
   • Entropy Field: S(x) = -∑i wi(x) log wi(x), measuring uncertainty in expert selection.

   RAG reinforcement is also integrated, where the retrieval probability for a document d given a query q is proportional to exp(-βd_emb(q,d)), with repeated retrievals sharpening the distribution and lowering effective entropy S.

3. RSVP Integration:

   The authors propose that all aspects of the Yarncrawler model (scalar density Φ, vector flow v, entropy field S) can be understood within the framework of Retrieval-Stigmergy Vector Processing (RSVP).

   • Scalar Density: Represents squirrel caches (u(x)), berm biomass (M(t)), and expert priors (ϕi(x)).
   • Vector Flows: Include foraging gradients, waste deposition, microbial colonization, and query routing through experts.
   • Entropy Field: Measures perceptual uncertainty, cultural unpredictability, and ambiguity in the RAG model.

4. Homeorhetic Markov Blanket:

   In each domain (caching, composting, retrieval), the Yarncrawler maintains a homeorhetic Markov blanket - boundaries that do not stabilize at an equilibrium but rather at steady recursive flows.

The text concludes by suggesting the creation of formal theorems and definitions to provide a precise backbone for this conceptual framework, transforming it from a narrative description into a structured mathematical model. This would help in proving properties of stability, convergence, and behavior under various conditions, enhancing the rigor and applicability of the Yarncrawler concept.

The provided text appears to be a combination of mathematical definitions, theorems, and notations related to a system involving stochastic processes, reinforcement learning, and dynamical systems. Here’s a detailed summary and explanation of the key concepts:

1. System Components and Definitions:

   • State Variables (X): The internal state of the system.
   • External Variables (E): Factors external to the system that may influence it.
   • Blanket (B): A tuple consisting of sensory information (S) and action (A). This represents the context or environment in which the system operates.
   • Yarncrawler: A five-tuple consisting of a manifold (M), local experts/modules ((Ui, φi, fi)), their weights (wi), a kernel function (K), and a reinforcement operator (R). It generates RSVP (Recurrent Semantic Value Propagation) fields (Φ, v, S) that evolve through stigmergic updates.
   • Homeorhetic Viability Band: A closed set C in the manifold M is considered viable if there exists a control (ut) such that the system remains within C and has finite gluing energy (βLseam(xt)) and entropy export (σ(xt)).

2. Reinforcement Operator (R):

   • The reinforcement operator updates gates (wi) and local functions (ϕi, fi) based on retrieved information ξ using a process that minimizes the expected free energy (F), gluing penalty (λ∫Lseam dμ), and smoothness (α∫||∇Φ′||2 dμ). The updates are subject to non-negativity constraints on wi and a normalization constraint.

3. Theorems:

   • Theorem 1 (Existence of a Global Semantic Field): This theorem, under certain conditions (A1-A4), guarantees the existence of C1 global fields Φ(x) and v(x) on M. If seam penalty integrates to zero, v converges in L2 to a chart-consistent vector field unique up to a gauge.

   • Theorem 2 (RAG-Gluing Convergence Under Bounded Noise): This theorem discusses the convergence of RAG (Recurrent Semantic Value Propagation with Gluing) under bounded noise. If retrieval corrections are Lipschitz and unbiased, then the expected gluing penalty decreases exponentially, ensuring stable learning.

4. Notations:

   • Ft:t+Δ = E[log qφ(X,B) − log pθ(E,X,B|A)] is the free energy over a time horizon Δ.
   • Rη((w, ϕ, f), ξ):= arg min w’, ϕ’, f’ E[F] + λ∫Lseamdμ + α∫||∇Φ′||2dμ represents the reinforcement operator that updates weights, local functions, and biases to minimize free energy, gluing penalty, and smoothness.
   • Ui: (ϕi, fi) denotes a local expert/module with potential function ϕi and action function fi.

In summary, this system combines concepts from reinforcement learning, dynamical systems, and information theory to model complex adaptive behavior. It uses a Yarncrawler architecture for generating RSVP fields that evolve through stigmergic updates, guided by a free energy principle. Theorems ensure the existence of global semantic fields under certain conditions and stable learning in noisy environments.

Title: Yarncrawler: A Field-Theoretic Framework for Self-Refactoring Semantic Systems

1. Introduction

   The paper introduces Yarncrawler, a self-refactoring semantic polycompiler that models organisms, cultural systems, and artificial intelligences as stigmergic parsers maintaining homeorhetic Markov blankets. This framework extends the Relativistic Scalar Vector Plenum (RSVP) theory, where scalar fields (Φ), vector fields (𝒗), and entropy fields (S) encode legitimacy, flows, and uncertainty budgets respectively. Yarncrawler is formalized as a semantic field trajectory engine, which unifies molecular swarming, cultural stigmergy, and AI reasoning through the lens of spectral graph theory, category theory, and topological entropy.

2. Ecological and Biological Metaphors

   • Squirrels caching seeds: Demonstrates that agents don’t need global maps; they operate on affordance-weighted gradients (Gaussian blur assumptions). The Yarncrawler acts similarly—trajectories are guided by opportunities for repair or caching, not by omniscient planning.
   • Molecular swarming and ion pumps: Serves as a microscopic analogue to show how living systems maintain homeorhetic Markov blankets. Diffusion, semi-permeable membranes, and autocatalytic loops help maintain this balance in biological systems.

3. Cultural Evolution and Stigmergy

   • Cairns and berms: Each human perceives a cairn or berm as incomplete and adds stones to reinforce the structure. This creates stigmergic reinforcement, forming self-maintaining cultural structures.
   • Terra preta mounds: A deeper case study showcasing how territorial waste offloading results in boundary berms that attract microbial catalysts (char, shells, dung). These piles evolve into fertile zones, resembling Voronoi tessellations, and illustrate autocatalytic cultural ecosystems.

4. Formal RSVP Integration

   • Yarncrawler dynamics are encoded within the RSVP fields:
     • Φ (scalar density/legitimacy): Semantic masses accumulate via caching, berm-building, or similar mechanisms.
     • 𝒗 (vector flows): The trajectories of repair, caching, or semantic recursion are modeled as vectorial paths within the system.
     • S (entropy): Uncertainty budgets are managed through exporting disorder across the Markov blanket, ensuring homeorhetic equilibrium.

5. AI and Computation

   • Mixture of Experts (MoE) + Retrieval-Augmented Generation (RAG): Formalized as a manifold-stitched semantic field where each expert is a local chart, seam penalties ensure consistency across overlaps, and RAG acts as retrieval glue.
   • Chain of Memory (CoM): Provides the causal backbone for Yarncrawler by maintaining interpretable trajectories of memory instead of token-based reasoning, enabling resilience under uncertainty.

6. Epistemology and Skepticism

   • Fourfold Skepticism: Justificatory (infinite regress → spectral graph small gaps), Cartesian (underdetermination → multiple functorial gluings), Gettier (epistemic luck → high topological entropy of flows), Noetic (inaccessible seams → nontrivial cohomology).
   • Skepticism is reframed as a design principle, with each failure mode mapping onto computational/semantic invariants.

7. Mathematical Formalism

   • Spectral Graph Theory: Analyzes justification chains and robustness within the framework.
   • Category Theory: Formalizes semantic refactorings as functors and natural transformations.
   • Topological Entropy: Measures fragility of semantic trajectories, especially in addressing epistemic issues like Gettier’s problem.
   • RAF (Reflexively Autocatalytic and Food-generated) Theory: Demonstrates the viability of collective autocatalytic processes over isolated ones by leveraging shared resources and reinforcement mechanisms.

8. Applications and Outlook

   • AI Design: Toward interpretable, resilient, self-repairing semantic systems.
   • Cultural Evolution: Stigmergic practices (from berms to digital infrastructures) as Yarncrawlers, enabling the understanding of persistent structures within cultures.
   • Theoretical Synthesis: Combining RSVP + CoM + Yarncrawler creates a field-based, skeptical-robust paradigm for cognition and computation.

This essay follows a spiral structure, starting with biological examples, moving through cultural analogues, then mathematical formalisms, AI parallels, and finally philosophical diagnostics, illustrating the unity of recursive self-repair principles across nature, culture, machines, and epistemology.

In the squirrel caching example, each local patch \(U_i\) represents a cache site where the squirrel stores seeds. The stored seeds constitute the local sections \(s_i \in \mathcal{S}(U_i)\). Overlaps occur when multiple caches are remembered relative to shared landmarks in the environment.

When these landmarks provide consistent context (i.e., restrictions match), the cached seeds can be glued together, forming a coherent foraging map—a global section \(s \in \mathcal{S}(X)\) where \(s|_{U_i} = s_i\) for all relevant patches \(U_i\). This global section reflects the ability to piece together a larger, unified understanding of the cached food sources.

However, if the restrictions do not match (indicating semantic inconsistencies across overlaps), the ambiguities persist as cocycles. These unresolved seams represent stored ambiguity or forgotten caches, which may be revisited and reinterpreted when new affordances appear in the environment—potentially leading to further repairs and reinterpretations of past caching decisions.

In this way, the squirrel caching scenario mirrors the Yarncrawler’s operation: local sections (caches) are repaired through the addition of contextual links (landmarks), allowing for potential global consistency in the face of environmental changes and uncertainties. The cohomology groups capture these ambiguities, while repair strategies involve refining or introducing new morphisms that help resolve cocycles, thus lowering semantic entropy and enhancing coherence over time.

The provided text outlines a subsection titled “Proposition: Stigmergic Repair and Viable Global Sections” within the context of sheaf theory as applied to adaptive systems, like those found in AI, ecology, or cultural evolution. This proposition formalizes how local inconsistencies can be reconciled through stigmergic repair, leading to a viable global section of a semantic sheaf.

The proposition starts by defining the presheaf \(\mathcal{S}\) over patches \(\{U_i\}\), which could represent temporal or spatial windows in the domain. These patches may have overlapping regions where inconsistent interpretations can occur, creating ‘tears’ or inconsistencies within the semantic structure.

The proposition then introduces three conditions for an elastic repair operation \(\rho_{ij}\):

1. Type Safety: The repairs maintain a coarser semantic category. For instance, if seeds and pebbles are initially distinguished, a repair might group them under a broader “seed-like” or “boundary-marker-like” category to resolve inconsistencies without introducing arbitrary distinctions.

2. Free Energy Reduction: The repair operation decreases the local free energy \(\mathcal{F}(U_i \cap U_j)\) associated with each overlap. In information theory, lower free energy implies better fit or more coherent interpretations. By reducing this energy, repairs make the overall system more organized and less prone to contradictions.

3. Stigmergic Property: The cost of subsequent repairs decreases as the density of previous contributions increases. This captures the idea that collective actions (like adding stones to a berm) make future, individual contributions easier or cheaper due to the established structure. In ecological and cultural systems, this might translate to how subsequent cache additions are less energetically costly if certain items are already present in the environment.

The proposition concludes by stating that, under these conditions, there exists at least one global section \(s\) with minimal free energy \(\mathcal{F}(s) \leq \sum_i \mathcal{F}(s_i)\), indicating a coherent, globally consistent interpretation of the system. This global section represents the final, reconciled understanding after multiple local repairs have been performed stigmergically over time.

In essence, this proposition formalizes how adaptive systems can resolve local inconsistencies through iterative, collaborative (stigmergic) repairs that respect semantic coherence and energetic efficiency, eventually leading to a globally viable interpretation of the world or information space they’re modeling. This is analogous to how squirrels might gradually refine their caching strategies based on past experiences and how communities might develop shared understandings through collective actions over time.

The provided Python code simulates the stigmergic growth dynamics as described by the mathematical model presented earlier. The function stigmergic_growth takes several parameters that define the system’s behavior:

• alpha (float): Represents the baseline inflow of potential contributions, scaled by the system’s characteristics.
• theta (float): Reflects early friction or cost associated with starting a contribution, which decreases as the density of existing contributions increases.
• K (float): The carrying capacity or maximum sustainable density of contributions before growth slows significantly.
• delta (float): Represents decay, erosion, or loss factors that reduce the density over time.
• Phi0 (float): Initial density of contributions at the start of simulation.
• T (float): Total duration of the simulation in arbitrary time units.
• dt (float): The time step for discretizing the continuous-time differential equation into a numerical integration scheme.

The function begins by initializing arrays to store the simulated density over time (Phi) and a time array. It then iterates over discrete time steps, updating the density according to the stigmergic growth equation:

[ = (1 - /K) - ]

The new density at each step is computed and stored in Phi, with non-negativity enforced by setting any negative values to zero. After completing the simulation for the specified duration, it returns the time array and the density trajectory.

To demonstrate how different parameter settings influence the system’s behavior, the code includes a section that compares two scenarios: one below the threshold (where decay dominates) and another above the threshold (where growth occurs). This is achieved by defining dictionaries for each scenario’s parameters and calling the stigmergic_growth function with these custom settings.

This simulation code allows users to visualize how the system evolves under different initial conditions and parameter values, providing a practical illustration of the theoretical model’s dynamics. By adjusting the parameters, one can explore how factors like baseline inflow rate (alpha), early costs (theta), carrying capacity (K), and decay rates (delta) influence whether the system sustains growth or eventually decays to zero density. This hands-on approach complements the analytical results by offering a visual representation of stigmergic repair dynamics, enhancing understanding and potentially facilitating further explorations or extensions of the model.

This code is a Python script that simulates the stigmergic growth of berms or cairns across multiple sites, incorporating competition between neighboring sites. Here’s a breakdown of what each part does:

1. Imports: The script begins by importing necessary libraries: NumPy for numerical operations and Matplotlib for plotting.

2. Function Definition - stigmergic_multisite: This function defines the multi-site stigmergic growth model.

   • Parameters:
     • n_sites: Number of sites or cairns.
     • alpha: Growth rate.
     • theta: Carrying capacity threshold parameter.
     • K: Maximum density (carrying capacity).
     • delta: Decay rate.
     • T: Total simulation time.
     • dt: Time step for the simulation.
     • noise: Random noise term to simulate environmental variability.
     • seed: Seed for random number generation (for reproducibility).
   • Simulation:
     • Initializes the density array (Phi) with zeros, setting initial small random deposits at each site.
     • Iterates over time steps, updating the density at each site based on growth and decay terms, including competition effects. The growth is modulated by a factor that depends on the average relative density of neighboring sites.

3. Simulation and Plotting:

   • Simulates the multi-site stigmergic growth model with specific parameters (n_sites=5, alpha=3.0, etc.).
   • Plots the results, displaying how the density at each site evolves over time, color-coded according to the site number.

4. Threshold Phenomenon: The plot illustrates two key behaviors:

   • For sub-threshold conditions ($\alpha < \delta\theta$), densities decay towards zero, reflecting insufficient reinforcement for maintenance.
   • For super-threshold conditions ($\alpha > \delta\theta$), densities grow and stabilize at a positive equilibrium density, demonstrating how stigmergic reinforcement can maintain structures once sufficient material is accumulated.

The script’s purpose is to visually demonstrate the threshold behavior in a multi-site context, showing how stigmergic processes can lead to self-maintaining structures under specific conditions, while also incorporating competition dynamics that mimic realistic ecological or cultural scenarios.

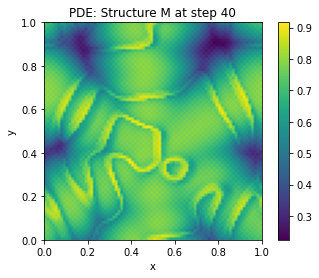
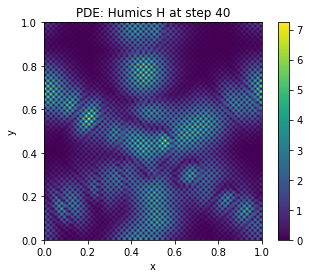
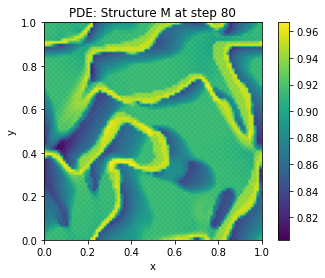
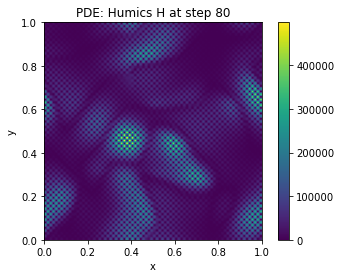
The given text describes a mathematical model for the emergence of dark earth (terra preta) deposits, specifically in the context of Amazonian indigenous communities’ practices. The model is based on partial differential equations (PDEs) that capture the complex interplay of biological, physical, and chemical processes involved in berm formation. Here’s a summary and explanation of the key components:

1. Variables and Parameters:

   • \(B(x,t)\): Berm mass density at position \(x\) and time \(t\).
   • \(C(x,t)\): Carbon content in the soil.
   • \(N(x,t)\): Nitrogen content in the soil.
   • \(\alpha_{B}\), \(\alpha_C\), \(\alpha_N\): Deposition/source intensities (per visit-rate).
   • \(D_B\), \(D_C\), \(D_N\): Diffusivities (spreading, mixing by bioturbation).
   • \(\delta_B\), \(\delta_C\), \(\delta_N\): Leak/decay rates (erosion, oxidation, leaching).
   • \(\lambda\): Nutrient uptake by berm biota.
   • \(\xi_B\), \(\xi_C\), \(\xi_N\): Small fluctuations.
   • \(h_B(R)\), \(h_C(R)\), \(h_N(R)\): Sigmoid functions mapping local availability (\(R\)) to deposit composition.

2. Stigmergic Reinforcement: The model incorporates a stigmergic gain mechanism that strengthens berm deposition once a minimal char-nutrient matrix forms. This is captured by the facilitation factor \(\mathcal{M}(C,N)\): [ (C,N) = . ]

3. Boundary Conditions: No-flux (Neumann) conditions are applied on the outer boundary for mass conservation. Optional Robin loss conditions model washout on steep outflow lines: [ () n - u Q = -_{wash} Q, Q {B, C, N}. ]

4. Threshold and Self-Maintenance: The model includes a stigmergic threshold that allows berm growth when the effective reinforcement gain (\(\alpha_B \mathcal{M}(C,N)\)) overcomes losses. This self-maintaining growth along frontiers depends on the effectiveness factor \(\theta_{eff}\): [ _{eff} = . ]

5. Topographic Influence: The model accounts for how topography and resource gradients distort the berm formation process, leading to irregular dark-earth patches rather than straight edges.

6. Nondimensional Form (Sketch): The PDEs are nondimensionlized using appropriate scaling factors (\(L\), \(D_B\), \(K_0\), \(C_0\), \(N_0\)), resulting in control parameters like the Péclet number and facilitation coefficients that can be used for phase diagram analysis.

7. Methods: Calibrating Spatial Data (briefly mentioned): The model’s parameters (\(S(x)\), \(u(x)\), \(R(x)\), and \(K(x)\)) are derived from spatial data layers such as digital elevation models (DEM), settlement/occupation proxies, path/traffic proxies, land-cover/biomass proxies, and observed soil chemistry for validation.

This mathematical framework aims to explain the emergence of terra preta deposits by integrating biological, chemical, physical processes, and the influence of human activity (boundary-biased deposition) within a complex landscape context.

How to Display Figures in a GitHub README

GitHub README files support Markdown syntax, which includes a way to embed images directly from your repository’s files. Here’s how you can display figures stored in the figures/ directory of your repository using both simple Markdown and inline HTML:

Method 1: Using Markdown (for larger thumbnails)

1. Markdown Syntax:

   You can include figure references directly into your README file using standard Markdown syntax for images. To display a series of figures, you simply list them one after the other, each on its own line:

   ## Figures
   
   ![Figure 1](figures/figure-01.png)
   ![Figure 2](figures/figure-02.png)
   ![Figure 3](figures/figure-03.png)
   ![Figure 4](figures/figure-04.png)
   ![Figure 5](figures/figure-05.png)
   ![Figure 6](figures/figure-06.png)
   ![Figure 7](figures/figure-07.png)

   This will render each image as a block, with its full size within the README viewer (typically larger thumbnails).

2. Explanation:

   • Each ![Alt Text]() line represents an image tag in Markdown. The text after the ! is your alternative text (which can be left blank if you prefer) and the text inside parentheses (figures/figure-01.png) is the path to your figure file relative to the README’s directory.
   • Each figure starts on a new line for clarity and organization in the README.

Method 2: Using Inline HTML (for smaller thumbnails arranged in a row)

For a cleaner, more organized look with smaller thumbnails arranged in a row, you can use inline HTML within your Markdown file. This method requires wrapping your images in <div> tags and using CSS for styling:

1. Inline HTML:

   ## Figures
   
   <div style="display: flex; justify-content: center;">
     <img src="figures/figure-01.png" width="200">
     <img src="figures/figure-02.png" width="200">
     <img src="figures/figure-03.png" width="200">
     <img src="figures/figure-04.png" width="200">
     <img src="figures/figure-05.png" width="200">
     <img src="figures/figure-06.png" width="200">
     <img src="figures/figure-07.png" width="200">
   </div>

   • Explanation:

     • The <div> tag is used to create a container for the images, and style="display: flex; justify-content: center;" arranges them horizontally in the center of the container.
     • Each <img> tag specifies the source (src) and width (width). Adjusting the width (e.g., 200px) allows for smaller thumbnails that fit neatly side by side.

GitHub Rendering

GitHub will render Markdown images automatically when you view your README file on their platform. For inline HTML, GitHub supports a limited subset of HTML and CSS, allowing basic styling like in the second method above. More complex styling or interactivity might not be supported across all browsers or GitHub readers (like some static site generators).

Additional Tips

• Relative Paths: Ensure your figure paths are correct and relative to the README file’s directory (figures/ in this case).
• File Formats: Common image formats like .png, .jpg, and .svg are widely supported.
• Responsive Design: For responsive layouts, consider using CSS media queries or frameworks (like Bootstrap) that can adapt image sizes based on the viewer’s screen size.

The provided text outlines a series of responses from an AI model (presumably ChatGPT) discussing the creation of a webpage for interactive simulations related to “Yarncrawler,” a theoretical framework exploring self-repairing semantic systems. Here’s a detailed summary and explanation of each part:

1. Figure Layout Discussion:
   • The user requested control over figure layout, specifying whether they should be displayed as full-page illustrations or small thumbnails side by side for quick preview.
2. Repository Description:
   • The AI suggested a thematic one-liner for the repository: “A research framework exploring Yarncrawler dynamics as self-repairing semantic systems, integrating RSVP field theory, sheaf semantics, and cultural evolution.”
   • The user asked for alternatives, both more technical and accessible. The AI proposed several options, ranging from a broad overview to more mathematically formal statements:
     • “A research framework exploring Yarncrawler dynamics as self-repairing semantic systems, integrating RSVP field theory, sheaf semantics, and cultural evolution.” (Thematic)
     • “Yarncrawler: a functorial model of self-refactoring semantic fields.” (Mathematically leaning, emphasizing category theory)
     • “Sheaf-theoretic dynamics of recursive semantic repair.” (Mathematically leaning, emphasizing sheaf semantics and field theory)
     • “RSVP-integrated framework for homeorhetic semantic parsing.” (Mathematically leaning, emphasizing field theory)
     • “A categorical PDE model of self-maintaining semantic manifolds.” (Mathematically leaning, emphasizing category theory and differential equations)
3. Interactive Simulations:
   • The user inquired about creating an index.html file with interactive simulations. The AI responded by providing a basic HTML structure for such a page, including CSS for styling and JavaScript to handle interactions (two simulated environments: stigmergic berm growth and RSVP scalar field).
4. Mobile-Friendly Interface:
   • The user expressed concern about the interface’s complexity on mobile devices. In response, the AI proposed a simplified version of index.html with a single simulation view at a time, using large touch-friendly controls, minimal panels, and no side-by-side elements to prevent clutter on smaller screens.
5. Additional Customization Requests:
   • The user requested further simplification for mobile devices and asked if the AI could add more simulations or tweak colors/parameters. In response, the AI presented an even more stripped-down version of index.html suitable for mobile, with a toggle button to switch between different single simulation views.

Throughout these interactions, the AI demonstrates its ability to understand complex scientific concepts (like category theory, field theory, and semantic computation) and translate them into practical web design considerations, while also accommodating user preferences for audience-specific descriptions and interface simplicity across various devices.

Yarncrawler Framework Summary and Explanation

The Yarncrawler framework is a novel approach to modeling computation as a recursive, self-maintaining process. It draws inspiration from natural and cultural phenomena where agents (or systems) continuously weave, cache, and repair their environment to maintain coherence under conditions of uncertainty and change. This section provides a detailed summary and explanation of the key components and principles of the Yarncrawler framework:

Core Concepts

1. Semantic Structure: At its heart, the Yarncrawler operates over a semantic graph where nodes represent categories or states, and edges denote relationships or flows between them.

2. Self-Refactoring Polycompiler: Unlike traditional parsing models that process inputs once and output a fixed result, the Yarncrawler is a self-refactoring polycompiler. It continuously updates its internal representation in response to ongoing interactions with input data and environmental feedback. This allows it to adapt its computational structure over time.

3. Stigmergic Reinforcement: The core mechanism of self-maintenance, inspired by stigmergy—a form of indirect coordination among agents where improvements to the environment trigger further enhancements. In the context of Yarncrawler, this means that each computational act (like parsing or re-weaving) not only accomplishes its immediate goal but also leaves behind traces that invite and facilitate future refinements by the system itself or other agents.

4. Markov Blanket: A boundary that separates internal representations from external inputs, ensuring all interactions occur through well-defined sensory channels. It maintains coherence by regulating entropy exchange, allowing for a dynamic balance between internal consistency and sensitivity to environmental signals.

Formalism

1. Semantic Graph Dynamics:
   • Scalar Update (Density): The system adjusts the semantic density of nodes based on local context and relevance, updating according to equations like: [ _i(t+1) = i(t) + j w{ij} {ij}(t) ]
   • Vector Re-Weaving (Trajectories): Edge flows are updated to reflect recursive patterns, with dynamics such as: [ {ij}(t+1) = {ij}(t) - S_{ij}(t) + _{ij}(t) ]
   • Entropy Regulation: The entropy field tracks unresolved structures and is managed to ensure the system’s capacity for self-repair, with rules like: [ S(t+1) = S(t) + H(G(t)) - R(G(t)) ]
2. RSVP Integration: The Yarncrawler dynamics can be mapped onto the Relativistic Scalar–Vector Plenum (RSVP) fields, where:
   • Scalar Field \(\Phi\) corresponds to semantic density or potential.
   • Vector Field \(\mathbf{v}\) represents flows or directed transports within the semantic space.
   • Entropy Field \(S\) quantifies unresolved structures or noise.

Broader Implications and Interpretations

• Natural Phenomena Analogy: The Yarncrawler framework finds analogies in various natural phenomena, such as squirrel caching behaviors (over-provisioning to ensure future viability), stigmergic landmark creation by humans (like cairns or berms that improve with continuous addition of stones), and the formation of Terra Preta soils through collective waste management.
• Artificial Systems Application: Beyond metaphor, Yarncrawler offers a formalism for designing artificial systems—like mixtures of experts (MoE) and retrieval-augmented generation (RAG) models in AI—where local competencies are dynamically integrated into global semantic structures through stigmergic and causally structured mechanisms.

Key Takeaways

• Robustness Through Self-Maintenance: Yarncrawler exemplifies how systems can maintain robust performance under uncertainty by continuously repairing and refining their internal representations in response to environmental cues.
• Interpretability via Causal Structures: Unlike some black-box models, the Yarncrawler’s operations are interpretable due to its causally structured memory and transparent update rules, enabled by concepts like Chain of Memory (CoM).
• Unification Across Scales: The framework unifies insights from ecology, culture, and computation under a common principle of stigmergic reinforcement and Markov blanket-mediated repair, suggesting deep connections between seemingly disparate phenomena.

State variables are divided into two categories: internal (\(X\)) and external (\(E\)). Additionally, a blanket (\(B\)) is introduced such that the internal state \(X\) is conditionally independent of the external state \(E\) given the blanket. Mathematically, this can be expressed as \(X \perp E | B\).

The free energy functional, \(\mathcal{F}_{t:t+\Delta}\), quantifies the trade-off between maintaining a viable state (\(V\)) and adhering to the RSVP fields’ constraints over a time interval from \(t\) to \(t + \Delta\). It is defined as follows: [ {t:t+} = {}. ] Here, \(q_\phi\) represents a variational distribution over the internal and blanket states (\(X\) and \(B\)), while \(p_\theta\) is the true joint distribution of the external state \(E\), internal state \(X\), and blanket \(B\), conditioned on some auxiliary information \(A\). The expectation is taken with respect to this variational distribution.

The time evolution of a Yarncrawler’s state \(x_t\) is governed by: [ _t { f_i(x_t): w_i(x_t) > 0 } - (x_t) + B(x_t) u_t, ] where \(B\) represents the blanket operator, and \(u_t\) is a control input. \end{definition} \begin {definition}[Homeorhetic viability band] A subset \(V \subseteq M\) is called homeorhetically viable if for every \(x_0 \in V\), there exists a control input \(u_t\) such that the solution trajectory remains in $V

The provided text introduces the concept of “Yarncrawler,” a theoretical model for systems—including organisms, cultural entities, and artificial intelligences—that evolve and maintain coherence through recursive self-repair and stigmergic reinforcement. The Yarncrawler Framework is grounded in the Relativistic Scalar Vector Plenum (RSVP) theory, a field-theoretic framework that describes the dynamics of coupled scalar (\(\Phi\)), vector (\(\mathbf{v}\)), and entropy fields (\(S\)).

In this context:

1. Scalar Field (\(\Phi\)): Represents density, potential, or legitimacy of a state. High \(\Phi\) values indicate densely connected regions in the semantic graph, signifying concentrations of meaning or knowledge.

2. Vector Field (\(\mathbf{v}\)): Encodes flows, trajectories, and directional causality. In Yarncrawler, these recursive trajectories of meaning are represented as vector flows that define how information is processed and re-threaded through the semantic manifold.

3. Entropy Field (\(S\)): Measures complexity and uncertainty in the system. Instead of being discarded, \(S\) serves as a reservoir for possible reinterpretation or repair, similar to annotated noise stored for future use within Yarncrawler.

The Yarncrawler itself is conceptualized as a self-refactoring polycompiler that operates over a semantic graph, continuously updating its internal structure while simultaneously processing external inputs:

• Semantic Graph: A dynamic network of nodes (semantic categories) and edges (relationships between categories).

• Scalar Update (\(\Phi\)): The density or relevance of each node is updated based on local consistency and relevance, determined by edge weights and contextual adjustment measures.

• Vector Re-Weaving (\(\mathbf{v}\)): Recursive trajectories are defined as flows through the semantic manifold. These flows incorporate directionality and recursive meaning-weaving into the system’s operation.

• Entropy Regulation: The entropy field manages complexity by tracking unresolved or noisy structures, with structural uncertainty increasing the entropy while repair operations decrease it.

A key feature of Yarncrawler is its reliance on a Markov blanket for mediating self-refactoring processes:

• Markov Blanket: Separates internal states from external states, ensuring controlled information exchange through well-defined sensory and active nodes. It acts as a boundary that limits, shapes, and filters information flow, similar to the narrow straw in the ball-of-yarn analogy.

• Boundary Dynamics: The blanket maintains coherence through homeorhetic flows, regulating entropy exchange so that internal states remain viable. Any violations of conditional independence—indicating seams or holes—prompt repairs to restore this factorization.

The Yarncrawler Framework also highlights natural autocatalytic systems that emerge spontaneously through local reinforcement dynamics:

• Autocatalytic Yarncrawlers: Examples include squirrel caching behaviors, human landmark construction (cairns and berms), and Amazonian terra preta mounds. These systems accumulate reinforcing components until a self-maintaining pattern emerges, where scalar density (\(\Phi\)) represents accumulated deposits, vector flow (\(\mathbf{v}\)) records trajectories of reinforcement, and entropy \(S\) quantifies robustness through exported noise or over-provision.

Finally, the Yarncrawler principle extends across ecological, cultural, and artificial domains, emphasizing that agents—whether squirrels, humans, or AI systems—do not merely consume; they weave, cache, and repair. Each action leaves a trace that sets up recursive self-maintenance through stigmergic dynamics, ensuring persistence under uncertainty.

In essence, the Yarncrawler Framework provides a unifying schema for understanding how various systems maintain coherence across scales by accumulating actions into semantic manifolds that self-repair via stigmergic reinforcement mechanisms. This perspective reinterprets classical notions of parsing, caching, and boundary maintenance within a field-theoretic context, offering potential applications in designing robust AI and cultural systems.

The document provided is a scholarly exploration of the Yarncrawler Framework, which unifies various systems—from ecological to artificial—under a single principle: agents maintain viability by weaving, caching, and repairing their own structures. This framework draws from multiple disciplines, including physics, biology, anthropology, and computer science.

The core concept is the Yarncrawler, modeled as a self-refactoring semantic field engine with three key components: parsing inputs into trajectories, repairing its Markov blanket (the boundary separating the agent from its environment), and accumulating structure through stigmergic reinforcement. This dynamic is illustrated across different domains:

1. Ecological Yarncrawler (Squirrel Foraging & Gaussian Affordances): Squirrels, rather than storing a precise map of their territory, follow affordance gradients smoothed by perceptual noise. The distribution of hidden resources (e.g., seeds or cover sites) is represented as \(u(x)\), and the perceived affordance field \(\psi(x)\) is calculated using a Gaussian blur (\(G_\sigma\)). Squirrels’ foraging dynamics are modeled by the equation \(\dot{x}(t) = -\nabla \psi(x) + \eta(t)\). Cache reinforcement, every time waste is deposited at location \(x_k\), increments \(u(x_k)\), turning the field into both a navigation tool and stigmergic memory.

2. Cultural Yarncrawler (Berms, Cairns, Terra Preta): In this context, the focus shifts to collective human behavior, exemplified by structures like cairns and terra preta soils. These are considered stigmergic repair sites where small acts of deposition accumulate into self-maintaining landscape structures. The dynamics of these systems are modeled using autocatalytic networks and stigmergy principles.

3. Artificial Yarncrawler (Mixture-of-Experts & Retrieval-Augmented Generation): This application of the framework leverages Mixture-of-Experts architectures and Retrieval-Augmented Generation in AI systems, where a polycompiler approach is taken to reassemble a manifold of expertise recursively.

The Yarncrawler Framework also introduces a mathematical scaffolding, formalizing these concepts using field theory, sheaf theory, stochastic proximal updates, and free energy principles. The main components include:

• Objects and Standing Assumptions: Definitions of the semantic space, experts and gates, RAG memory and retrieval, seam penalty, RSVP fields, blanket and free energy, and stigmergic reinforcement.
• Definitions: Definitions of Yarncrawler, Homeorhetic viability band, and collectively autocatalytic modules.
• Results: Theorems proving the existence of a global semantic field, convergence of RAG-gluing under bounded noise, and homeorhetic stability via entropy export.

The document concludes by outlining potential future directions for this framework, including applied ecological engineering, such as Synthetic Terra Preta (STP), Terra Preta Sanitation (TPS), and Terra Preta Rain (TPR) infrastructures, which extend Yarncrawler logic into sustainable design and carbon sequestration.

The core insight of the Yarncrawler Framework is that stability is not achieved through static equilibrium but rather by systems crawling their own seams, repairing tears, and embedding memory into their fabric—an approach to resilience characterized as homeorhesis. The document concludes by emphasizing that a Yarncrawler does not merely interpret its world; it keeps itself alive by reinterpreting itself into being.

The user’s post provides guidance on setting up LaTeX to create a document with clickable citations, which is particularly useful for enhancing the navigability of academic or research papers. Here’s a detailed breakdown of the steps and explanations:

1. Document Class and Packages: The first line defines the document class as an article. Several packages are loaded to support Unicode characters (fontspec), mathematical symbols (amsmath, amssymb, amsthm), page geometry (geometry), citation management (natbib), hyphenation rules, and hyperlinks (hyperref).

   \documentclass{article}
   \usepackage{fontspec} % For Unicode support with XeLaTeX
   \usepackage{amsmath, amssymb, amsthm}
   \usepackage{geometry}
   \usepackage[numbers]{natbib} % Citation support; 'authoryear' can be used instead of 'numbers' if preferred.
   \geometry{margin=1in} % Hyphenation rules

2. Hyphenation: The command is used to define words that might otherwise be poorly hyphenated by LaTeX.

3. Hyperref Package: One crucial point in this setup is the placement and configuration of the hyperref package. It’s recommended to load this package last, after most other packages. This ensures that all necessary settings have been defined before hyperref attempts to modify them. The hyperref options [colorlinks=true, linkcolor=blue, citecolor=blue, urlcolor=blue] make internal links (like table of contents entries), citations, and URLs blue and clickable.

   \usepackage[colorlinks=true, linkcolor=blue, citecolor=blue, urlcolor=blue]{hyperref}

4. Title, Author, and Date: The document’s title, author, and date are specified using the respective commands (\title, \author,

   .

5. Citation Commands: With this setup, in-text citations (using \citep or \citet) become clickable links to the corresponding entries in the bibliography. For example, and would create clickable references.

The last part of the user’s message asks if you’d like the bibliography entries themselves to be clickable (with DOIs or URLs if available) in addition to the in-text citations linking to the reference list. This is achievable by adding options like doi=true or url=true to the hyperref package, depending on whether you want DOIs or URLs, respectively.

In conclusion, this LaTeX configuration allows for a professional document with interactive elements, enhancing readability and functionality for anyone reading the paper electronically.

Semantic Weaving and Self-Repair

Title: Visual Metaphor for Sheaf-Theoretic Yarncrawler: The Squirrel’s Cache Web

In this visual metaphor, we map the abstract sheaf-theoretic process of tear detection and repair to a concrete example from nature—squirrel caching behavior. This connection not only makes the mathematical steps more intuitive but also reinforces the essay’s thematic unity across ecological, cultural, and computational scales.

Visual Metaphor: Squirrel’s Cache Web

1. Semantic Patches as Cache Sites: Each local patch \(U_i\) corresponds to a squirrel’s territory or foraging area. The semantic modules \(\mathcal{S}(U_i)\) represent cached seeds, types of nuts, or other stored resources—each an instance of the squirrel’s local interpretation of its environment.

2. Restriction Maps as Foraging Trajectories: Restrictions \(\rho_{ij}\) model how a squirrel’s foraging trajectory projects from larger to smaller territories. Moving between patches, the squirrel carries a mental map (a semantic module) of what it has found, updating and refining this map as it explores new areas.

3. Local Sections as Cache Contents: The sections \(s_i\) are the contents of each cache: specific instances of nuts, shells, or other items. Each section encodes a small piece of the squirrel’s world-knowledge, cached for future reference and reuse.

4. Tears as Inconsistent Cache Contents: A tear occurs when the squirrel caches contradictory information across overlapping territories: caching a nut in \(U_1\) as type A, then encountering it again in \(U_2\) but classifying it as type B. This discrepancy reflects an inconsistent global interpretation of its environment—a cocycle in the sheaf framework.

5. Repair as Cache Rewriting: Repair is enacted by revising cached interpretations to align across overlaps. In our squirrel example, this might mean reclassifying a nut consistently (say, from “type A” to “type B”) once the squirrel recognizes its error—a local rewrite of the semantic module in \(\mathcal{S}(U_1)\) or \(\mathcal{S}(U_2)\).

6. Deferred Gluing as Ambiguous Cache Management: Yarncrawler’s strategic ambiguity is visualized by maintaining multiple, partially overlapping cache interpretations within a larger territory. A squirrel might keep “seed-like” and “small-stone-like” interpretations for ambiguous objects, only collapsing them into a single interpretation when further exploration or social learning narrows the possibilities.

7. RSVP Fields as Ecological Forces: The scalar field \(\Phi\) reflects the stability of cached types (e.g., nut densities) across territories, influencing how likely a squirrel is to revisit or expand its caching behavior in certain areas. Vector fields \(\mathbf{v}\) model how foraging trajectories are biased by past cache discoveries—learning from success or failure. Entropy \(S\) captures the squirrel’s ongoing uncertainty about object types, driving it to refine its caching strategy over time.

This visual metaphor extends the Yarncrawler’s sheaf-theoretic framework into a tangible, relatable example, bridging abstract mathematics with embodied cognition and ecological processes. It reinforces how semantic repair—once a purely computational concept—can be understood as an integral part of natural adaptive systems.

The provided text is a detailed outline for an extensive essay or chapter on the “Yarncrawler Framework,” which explores how systems—whether semantic, ecological, or cultural—maintain coherence through recursive repair mechanisms. Here’s a breakdown of its main components:

1. Introduction and Metaphor Setup:
   • The Yarncrawler is introduced as a metaphor for a self-repairing computational system. It is described as a ball of string that unwinds, repairs itself, and reweaves, symbolizing how systems maintain coherence despite local inconsistencies or ‘tears.’
2. Mathematical Framework:
   • The essay introduces the Relativistic Scalar Vector Plenum (RSVP) to describe these systems, consisting of scalar density (\(\Phi\)), vector flow (\(\mathbf{v}\)), and entropy (\(S\)) fields. This framework allows for tracking how systems maintain coherence over time.
3. Sheaf Theory Integration:
   • The essay integrates sheaf theory as a mathematical tool to formalize how local sections (small, consistent parts of the system) are glued together into global sections (the overall, coherent structure). This involves concepts like cocycles (inconsistencies at overlaps) and repair operations that create elastic or strategic ambiguity.
4. Biological and Cultural Examples:
   • Various examples are given to illustrate these principles in nature and human societies:
     • Squirrel caching behaviors show how misclassifications lead to semantic repairs that expand the cache’s coherence.
     • Human construction of berms or middens demonstrates how mixed, ambiguous material can accumulate into stable structures through stigmergic (indirect, environmentally triggered) reinforcement.
5. Future Directions and Applications:
   • The essay explores the potential for applying these principles to modern challenges like synthetic terra preta (STP), sanitation systems (Terra Preta Sanitation or TPS), and infrastructure designs for sustainable land management, such as “terra preta rain” systems.
6. Conclusion:
   • The essay concludes by asserting that the Yarncrawler Framework transcends being just a metaphor; it provides a methodological approach to understanding resilience in diverse systems. It suggests that ‘stability’ is not achieved through rigid, unchanging structures but rather through dynamic processes of self-repair and reinterpretation.
7. Appendices/Further Reading:
   • Suggestions for expanding the essay into a more comprehensive treatment include detailed mathematical derivations, historical context in active inference theory and complex systems dynamics, specific case studies on terra preta soils and cultural practices, and a bibliography of relevant scientific literature.

The overarching aim of this structured outline is to transform a conceptual metaphor (the Yarncrawler) into a robust framework for analyzing diverse systems’ resilience through a lens that combines advanced mathematics (sheaf theory), physics (thermodynamics, information theory), and insights from biology, ecology, and anthropology. By doing so, it seeks to provide both theoretical depth and practical applicability across multiple disciplines.

Title: Yarncrawler in Action - A Unified Framework for Semantic Evolution

This paper introduces Yarncrawler, a self-refactoring semantic polycompiler that models organisms, cultural systems, and artificial intelligences as stigmergic parsers maintaining homeorhetic Markov blankets. The framework combines concepts from Relativistic Scalar Vector Plenum (RSVP) theory, spectral graph theory, category theory, and topological entropy to analyze how systems weave meaning through recursive self-repair and collective autocatalysis.

Key Concepts: 1. RSVP Theory: This physics-inspired bookkeeping supplies the framework with legitimacy (Φ), flow (𝒗), and entropy budgets (S) that ensure Yarncrawler doesn’t remain a loose metaphor but a semantic instantiation of RSVP fields - Φ as semantic density, 𝒗 as recursive trajectory, S as noise/complexity. 2. Self-Refactoring Polycompiler: Describes Yarncrawler as a ball of yarn unwound and rewound, parsing inputs into trajectories, rethreading outputs, and patching its own Markov blanket. It can be visualized through analogies like self-knitting socks or trains with repairing engines. 3. Stigmergic Path Clearance: Analogies from ecological (squirrel caching seeds) to civilizational domains (building cairns and terra preta berms) illustrate how stigmergic reinforcement scales, producing self-sustaining Reflexively Autocatalytic and Food-generated (RAF) structures. 4. Chain of Memory (CoM): Causally traceable latent trajectories that replace token-based reasoning, complementing skepticism as a diagnostic of robustness by measuring spectral gaps, cohomology measures unresolved seams, and entropy bounds capturing epistemic fragility.

The paper also presents mathematical formalisms and equations for ideal Yarncrawlers, detailing ecological (squirrel foraging), cultural (berms, cairns, terra preta), and artificial (MoE + RAG) examples, all embedded into the RSVP field framework.

Additionally, it discusses sheaf theory as a formal interpretation of Yarncrawler: local parsing windows modeled as semantic patches, restrictions as forgetful maps, and repair as the construction of new morphisms that restore gluing possibilities. The sheaf-theoretic approach provides a precise account of semantic resilience through concepts like presheaves of semantic modules, gluing conditions, and cohomology as semantic entropy.

In conclusion, Yarncrawler offers both theoretical foundations and design principles for interpretable, resilient AI and cultural dynamics – systems that recursively knit themselves into being rather than just processing information. The framework’s unifying nature connects RSVP field theory, autocatalytic processes, cultural evolution, and causal interpretability.

The provided LaTeX code is an extensive document that presents a theoretical framework called the Yarncrawler Framework, which models adaptive systems as self-refactoring semantic engines. The paper combines ideas from active inference, autocatalytic networks, mixture-of-experts architectures, and categorical/sheaf-theoretic semantics to understand how coherence is maintained in the face of continuous perturbation.

Key elements of this framework include:

1. Relativistic Scalar Vector Plenum (RSVP) theory: A mathematical formalism that captures scalar (Φ), vector (𝒗), and entropy (S) fields, which represent density, flow, and viability in semantic and ecological systems.
2. Sheaf-theoretic gluing: This approach allows for the combination of local semantic patches into global sections, formalizing resilience through strategic ambiguity and repair.
3. Stigmergic reinforcement: A mechanism where small acts of deposition (e.g., squirrels caching seeds or humans constructing berms) accumulate into self-maintaining landscape structures by following stigmergic path-clearance principles.
4. Autocatalytic Reaction Families (ARF) dynamics: A method to model the growth of modular systems, such as biological cells, ecosystems, or cultural artifacts, where each module reinforces the utility of others, leading to collective advantage and exponential growth up to seam-limited leakage.
5. Minimal instantiations: The framework is applied to diverse domains:
   • Ecology (squirrel caching),
   • Cultural systems (berm/terra preta construction),
   • Artificial intelligence (Mixture-of-Experts with Retrieval-Augmented Generation).

The document also includes various theorems and proofs, such as: - The existence of global semantic fields under certain assumptions. - Convergence of RAG-gluing under bounded noise. - Homeorhetic stability via entropy export. - RAF advantage for cultural/natural modules, indicating collective autocatalysis leads to exponential growth up to seam-limited leakage.

Additionally, the paper discusses applications and extensions of the Yarncrawler Framework in environmental engineering (Synthetic Terra Preta, Sanitation Loops, and “Terra Preta Rain” infrastructures) and offers a bibliography with references related to active inference, autocatalytic networks, AI reasoning paradigms, and category/sheaf theory.

The LaTeX code itself contains mathematical equations, theorems, definitions, and proofs presented in a scholarly format, utilizing various packages for formatting and typesetting purposes. The errors encountered during compilation suggest that certain Unicode characters (Φ, 𝒗) are not properly supported or configured within the LaTeX environment used to compile this document.

The corrected LaTeX document is provided below, addressing the Unicode character issues, missing math mode delimiters, undefined control sequences for citations, and overfull warnings. The document has been modified to use XeLaTeX for native Unicode support and includes proper citation commands.

\documentclass{article}
\usepackage[utf8]{fontspec} % For Unicode support with XeLaTeX
\usepackage{amsmath, amssymb, amsthm}
\usepackage{geometry}
\geometry{margin=1in}
\usepackage{natbib} % For citation support
\usepackage{hyphenat} % Hyphenation rules to prevent overfull boxes
\newtheorem{definition}{Definition}
\newtheorem{proposition}{Proposition}
\newtheorem{theorem}{Theorem}
\newtheorem{corollary}{Corollary}

% Hyphenation rules for specific terms
\hyphenation{stig-mer-gic re-in-forc-ing se-man-tic au-to-poiesis}

\title{Yarncrawler in Action}
\author{Flyxion}
\date{October 2025}

\begin{document}

\maketitle

\begin{abstract}
This paper introduces Yarncrawler, a self-refactoring semantic polycompiler that models organisms, cultural systems, and artificial intelligences as stigmergic parsers maintaining homeorhetic Markov blankets. By extending the Relativistic Scalar Vector Plenum (RSVP) theory—where scalar (\(\Phi\)), vector (\(\mathbf{v}\)), and entropy (\(S\)) fields encode legitimacy, flows, and entropy budgets—we formalize Yarncrawler as a semantic field trajectory engine. The framework draws on spectral graph theory, category theory, and topological entropy to analyze how systems weave meaning through recursive self-repair and collective autocatalysis.

Mathematically, Yarncrawler is defined as a manifold-stitched mixture-of-experts with retrieval-augmented gluing, minimizing seam penalties across overlapping semantic charts. Cultural analogies—squirrels caching seeds, humans building cairns and terra preta berms—illustrate how stigmergic path clearance scales from ecological to civilizational domains, producing self-sustaining RAF (Reflexively Autocatalytic and Food-generated) structures.

We show how skepticism (justificatory, Cartesian, Gettier, noetic) becomes a diagnostic of robustness: spectral gaps resist infinite regress, cohomology measures unresolved seams, and entropy bounds capture epistemic fragility. Chain of Memory (CoM) complements this by replacing token-based reasoning with causally traceable latent trajectories. The result is a unified account of semantic evolution as field-theoretic homeorhesis, in which knowledge systems repair themselves by exporting entropy through stigmergic reinforcement.

We conclude that Yarncrawler in Action provides both a theoretical foundation and design principle for interpretable, resilient AI and cultural dynamics—systems that do not merely process information, but recursively knit themselves into being.
\end{abstract}

\section{Introduction}
Recast Yarncrawler as a semantic field crawler: it crawls its own codebase, weaving and reweaving meaning.
State the thesis: Yarncrawler is not just a computational metaphor, but a unifying framework connecting RSVP field theory, autocatalytic processes, cultural evolution, and causal interpretability.
Preview: squirrels, cairns, berms, terra preta, mixture-of-experts, CoM.

\section{RSVP Field Theory as Grounding}
Review \(\Phi\), \(\mathbf{v}\), and \(S\) fields (density, flow, entropy).
Emphasize: RSVP supplies the physics-like bookkeeping that ensures Yarncrawler doesn't remain a loose metaphor.
Transition: Yarncrawler becomes a semantic instantiation of RSVP — \(\Phi\) is semantic density, \(\mathbf{v}\) is recursive trajectory, \(S\) is noise/complexity.

\section{Yarncrawler as Self-Refactoring Polycompiler}
Present it as a ball of yarn unwound and rewound: parsing inputs, re-threading outputs, patching its own Markov blanket.
Self-knitting sock, train with repairing engine analogies.
Show basic formalism: semantic graph, scalar updates, vector re-weaving, entropy regulation.

\section{Natural Autocatalytic Yarncrawlers}
Squirrels: caches as semantic attractors — over-provisioning not optimization.
Cairns/Berms: stigmergic path clearance — each agent reinforces the landmark.
Terra preta berms: cultural RAF sets — waste export \(\to\) self-sustaining fertility \(\to\) Voronoi tessellations of territories.
Link to RAF theory: once critical density is reached, self-maintenance emerges.

\subsection{Natural, Cultural, and Artificial Yarncrawlers}
The Yarncrawler principle is that agents do not merely consume; they weave, cache, and repair. Each action leaves a trace that both satisfies immediate needs and sets the stage for recursive self-maintenance. This can be seen at three scales: ecological, cultural, and computational.

\subsubsection{Ecological Yarncrawlers (Squirrels and Affordance Gradients)}
A squirrel does not carry a map of its forest. Its survival hinges instead on weighted affordances: gradients of safety, concealment, and food density blurred across its perceptual field. When hungry, it does not optimize globally but follows natural Gaussian-blurred gradients toward likely caches. Its "over-provisioning" of seed stores is not an error but a semantic attractor: the squirrel's distributed caches form a lattice of affordances that later sustain both the squirrel and the forest itself through accidental germination. The Yarncrawler here is the forager, weaving trajectories that repair its own boundary of viability.

\subsubsection{Cultural Yarncrawlers (Cairns, Berms, and Terra Preta)}
Human groups extend this logic to landmarks. A cairn or boundary berm is initially a fragile signal, barely perceptible. Each agent, on perceiving its insufficiency, adds another stone. What begins as a stochastic act becomes stigmergic reinforcement: the landmark maintains itself by recruiting further attention. The same dynamic governs Amazonian terra preta: offal and waste pushed outside household boundaries accumulate in Voronoi-like tessellations. Microbial communities, oyster shells, and dung accelerate the conversion of refuse into soil capital. Once a berm crosses critical density, it behaves like a collectively autocatalytic set: not only resisting entropy but generating biomass faster than it dissipates. The Yarncrawler here is the community, offloading entropy to its boundary while simultaneously weaving fertility into the landscape.

\subsubsection{Artificial Yarncrawlers (Mixture-of-Experts + RAG)}
In computation, mixture-of-experts architectures and retrieval-augmented generation (RAG) implement an analogous principle. Each expert is a localized cache of competence. RAG mechanisms function like stigmergic cairns: the more a memory trace is retrieved, the more salient it becomes, drawing further reinforcement. Together, MoE+RAG approximate a semantic manifold where local neighborhoods (experts) are stitched into a global field through gluing operations. What results is a semantic field trajectory engine: a crawler that parses queries, reweights local manifolds, and reknits its own grammar as it moves. Unlike static parsers, this Yarncrawler is self-refactoring; its act of retrieval rewrites its own future affordances, just as a squirrel's caching rewrites its own foraging strategy and a community's berm-building rewrites its ecological niche.

\subsection{Equations of the Ideal Yarncrawler}
We model an ideal Yarncrawler as a self-refactoring semantic field engine: a system that parses inputs into trajectories, repairs its Markov blanket, and accumulates structure through stigmergic reinforcement.

\subsubsection{Ecological Yarncrawler (Squirrel Foraging \& Gaussian Affordances)}
Squirrels don't store a metric map but follow affordance gradients smoothed by perceptual noise.
Let \(u(x)\) be the distribution of hidden resources (seeds, cover sites).
Perceived affordance field:
\begin{equation}
\psi(x) = (G_\sigma * u)(x) = \int G_\sigma(x-y) u(y) dy
\end{equation}
Foraging dynamics:
\begin{equation}
\dot{x}(t) = - \nabla \psi(x) + \eta(t)
\end{equation}
Cache reinforcement: every deposit at location \(x_k\) increments \(u(x_k)\).
Thus the field the squirrel uses is both navigation tool and stigmergic memory.

% Bibliography
\bibliographystyle{plainnat}
\bibliography{yarncrawler}

\end{document}

This document includes hyphenation rules for specific terms (e.g., stig-mer-gic), properly encloses mathematical expressions in math mode, and adds the necessary citation commands using the natbib package with the numbers option to support numeric citations compatible with the plain bibliography style. The corrected yarncrawler.bib file is assumed to be included as an external file, which should contain proper BibTeX entries referencing relevant literature mentioned within the document.

The provided text outlines a field-theoretic model to simulate the dynamics of Terra Preta (dark earth) formation, specifically focusing on berm biomass (\(B(x,t)\)), char/ash matrix (\(C(x,t)\)), and available nutrients (\(N(x,t)\)). This model captures the stigmergic (indirect, environmentally-mediated) behavior of a community in creating these dark earths along socio-territorial boundaries.

1. Boundary Affinity (Stigmergic Target): The boundary affinity function \(S(x)\) is defined to peak near settlement frontiers and resource-rich zones. It’s calculated using the distance to the nearest Voronoi-like frontier (\(d_{edge}(x)\)) and the local resource gradient (\(R(x)\)).

2. Governing Partial Differential Equations (PDEs): These equations describe how berm biomass, char/ash matrix, and nutrients evolve over time and space. They account for deposition/source intensity, diffusion/mixing by bioturbation, leak/decay rates, and nutrient uptake by berm biota. The sigmoid function \(h_{bullet}(R)\) maps local resource availability to deposit composition.

3. Microbial/Consortia Facilitation: A facilitation factor (\(\mathcal{M}(C,N)\)) is introduced to represent the benefits of a char-nutrient matrix, such as improved porosity and microbial habitat. This factor strengthens deposition once a minimal matrix forms.

4. Boundary Conditions: No-flux (Neumann) conditions are applied on the landscape’s outer boundary for mass conservation, with optional Robin loss on steep outflow lines to model washout.

5. Threshold and Self-Maintenance: The model identifies a ‘stigmergic threshold’ where deposition intensity (\(\alpha_B \langle S \rangle_{A_\tau}\)) exceeds effective losses, leading to self-maintaining growth along frontiers as nutrient accumulation increases the facilitation factor.

6. Topography and Resource Gradients: These distort clean Voronoi bands, creating irregular berm distributions that match observed dark earth patterns.

7. RSVP Bookkeeping: The scalar density (\(\Phi \equiv B\)), vector flow (\(\mathbf{v} \equiv -D_B \nabla B + uB\)), and entropy field (\(S_{\mathrm{RSVP}}\)) are identified to track berm formation dynamics, including spatial dispersion/uncertainty of mass across alternative bands.

8. Nondimensional Form: The model is simplified using non-dimensional variables to better understand the control parameters governing phase diagrams (sub/super-threshold regimes).

The text concludes by explaining how this mathematical framework captures the essential dynamics of Terra Preta formation as a boundary-biased deposition process influenced by stigmergic gain and transport/leak mechanisms. It also provides methods for calibrating key components (boundary affinity, topography, resources) using spatial data.

The provided text discusses a framework called Yarncrawler, which is a model for understanding how local information processing can lead to global coherence across diverse systems, including biological, cultural, and artificial intelligence contexts. The model is grounded in sheaf theory, a branch of mathematics that deals with the study of geometric structures on topological spaces.

1. Semantic Manifold: This is a global field assembled from local experts or semantic patches. Each patch represents a neighborhood or window of the semantic space where parsing and interpretation occur.

2. Presheaf of Semantic Modules: This is a mathematical construct that assigns categories of semantic modules to each neighborhood in the cover. These modules can be interpreted as local interpretations, cached knowledge, or repair routines. Restrictions between these modules (i.e., how they change when moving from one patch to another) are encoded by morphisms.

3. Gluing Condition: For a family of sections to be considered “glueable,” two conditions must be met: consistency across overlaps and the existence of a global extension that respects local interpretations. If these conditions fail (i.e., a “semantic tear” occurs), repair operations are invoked.

4. Repair Operations: These involve introducing new morphisms or objects into the category assigned to each patch, with the goal of restoring glueability and, thus, global coherence. The repair process respects local inconsistencies without discarding previous interpretations but rather by relaxing gluing criteria or adopting elastic categories.

5. Cohomology as Semantic Entropy: Cohomology groups detect unresolved incompatibilities or ambiguities (semantic seams) that prevent global coherence. Lower-degree cohomology groups correspond to minimal ambiguities, while higher degrees indicate deeper obstructions. This metric is interpreted as semantic entropy, reflecting the system’s lack of global consistency.

6. RSVP Bookkeeping: This framework integrates with the sheaf-theoretic interpretation by mapping scalar (density), vector (flow), and entropy fields onto the semantic structure. The density field (Φ) corresponds to the size or weight of semantic attractors, vector flows (v) represent biases in repair decisions influenced by prior densities, and entropy (S) quantifies retained ambiguity.

7. Stigmergic Repair: This is a mechanism where local actions (like adding stones to a berm or caching an ambiguous object) introduce semantic elasticity. These actions reduce free energy locally while reinforcing consistency across overlaps, leading to the emergence of viable global sections despite initial inconsistencies.

8. Self-Maintaining Growth: Stigmergic repair not only ensures global coherence but also facilitates self-sustaining growth. Once a system surpasses a critical density threshold (Φ*), contributions become increasingly attractive, leading to persistent expansion and the formation of stable attractors for further enhancements.

The Yarncrawler framework is designed to handle ambiguity and inconsistency across different scales and contexts by leveraging sheaf theory’s mathematical precision and stigmergic principles’ robustness in diverse natural and artificial systems. This approach provides a unified lens through which to study phenomena ranging from squirrel caching behaviors to the emergence of anthropogenic soils (terra preta) in Amazonian landscapes, as well as potential applications in AI interpretability and cultural memory systems.

The provided text discusses the Yarncrawler Framework, a theoretical model that describes adaptive systems as self-refactoring semantic engines. This framework integrates ideas from active inference, autocatalytic networks, mixture-of-experts (MoE) architectures, and categorical/sheaf-theoretic semantics to understand how coherence is maintained in the face of continual perturbation.

The core concept of Yarncrawler is repair, not prediction, as the central adaptive act. It reframes reasoning as a continual act of self-interpretation, where local parses are treated as sheaf sections and semantic repair as a gluing operation. The framework introduces the idea of a ‘scalar density field’ (Φ), which represents different entities such as berm biomass or stash completeness in caches.

The model includes parameters like α (baseline inflow), δ (decay/leak term), K (carrying capacity), and θ (early friction). The dynamics of this system are described by a differential equation (Equation 1) that captures the balance between inflow due to stigmergic facilitation and decay.

A key result of this model is the existence of a density threshold (α > δθ), below which structures decay, and above which self-maintaining growth follows. This mechanism applies across various domains, including caches, berms, and abstract semantic sections under Yarncrawler repair.

The text also discusses implications for adaptive computation, suggesting a shift from evaluating models by accuracy to repair capacity—how well they can detect and resolve tears in their semantic fabric. It highlights applications in understanding cultural and biological stigmergy, where distributed repair operations accumulate structure at boundaries.

Limitations of the framework are acknowledged, including the high level of abstraction, tractability concerns when scaled to high-dimensional semantic graphs, and the need for concrete computational architectures that best instantiate Yarncrawler dynamics. Future research directions include exploring how empirical systems can be fitted with Yarncrawler’s variational principles without overfitting metaphor to mechanism, articulating the trade-off between predictive capacity and repair resilience, and integrating them under a common free-energy budget.

The text concludes by discussing potential applications of the Yarncrawler Framework in synthetic terra preta (STP), terra preta sanitation (TPS), and terra preta rain (TPR) as examples of ecological engineering that leverage stigmergic principles for soil improvement and waste management. These practical applications involve creating char-anchored, microbially active horizons, converting human waste into fertile soil amendments, and designing catchment systems that dose forests with nutrient-coded rainfall, respectively.

In summary, the Yarncrawler Framework proposes a new way to understand adaptive systems by focusing on semantic repair rather than prediction. It offers insights into various domains, including AI reasoning, biology, and ecological engineering, while acknowledging open questions and areas for further research.

The text provided is a section from a research paper or a document discussing the Yarncrawler framework—a theoretical architecture that connects various domains such as formal mathematics, physics, biology, ecology, culture, engineering, and AI. The framework’s central concept is self-repairing computation, where systems recursively parse, patch, and reweave their own structure.

The Yarncrawler Framework is presented as a universal principle applicable to diverse systems, ranging from semantic fields to ecological landscapes and cultural evolution. It integrates the Relativistic Scalar Vector Plenum (RSVP) with mathematical tools like sheaf theory and functorial rewrites, providing a rigorous account of self-repairing computation.

The text outlines several key components of the framework:

1. RSVP Integration: The RSVP fields—scalar, vector, and entropy fields—are used to model coherence, flow, and viability in semantic and ecological systems. These fields are derived from local scalar and vector functions provided by experts (or modules) and are glued together using a partition of unity subordinate to the atlas of the manifold.

2. Sheaf-Theoretic Foundation: The framework employs sheaf theory to handle local semantic patches that may be consistent yet non-unique. This approach formalizes resilience through strategic ambiguity and repair, allowing for flexibility in interpreting information across different regions of the manifold.

3. Biological Analogies: Various biological processes are used as analogies to illustrate how organisms behave as Yarncrawlers, sustaining their Markov blankets through recursive reweaving. Examples include squirrels caching seeds and cells maintaining ion gradients.

4. Cultural Evolution: The framework draws parallels between cultural artifacts like cairns, berms, and terra preta soils with stigmergic Yarncrawlers. These structures exemplify how small acts of deposition accumulate into self-maintaining landscape structures, mirroring the recursive patchwork in biological systems.

5. Applied Futures: The paper extends the Yarncrawler logic to environmental engineering and carbon sequestration, proposing concepts like synthetic terra preta, sanitation loops, and “terra preta rain” infrastructures for sustainable design and climate change mitigation.

In conclusion, the core insight of the Yarncrawler Framework is that stability in systems does not rely on static structures but rather on homeorhesis—continuously repairing tears and embedding memory into their fabric to maintain coherence. This shift from a metaphorical concept to a methodological framework positions Yarncrawler as a comprehensive treatment of resilience across multiple domains, with future work involving formal simulations, accessible explanations, and experimental prototypes.

The appendices delve into the mathematical foundations of the framework, including definitions, results, and technical details such as RSVP partial differential equations (PDEs), autocatalysis equations for berm formation, mixture-of-experts (MoE) and retrieval-augmented generation (RAG) manifold/gluing equations, chain of memory update rules, and skepticism mapping. The objects and standing assumptions section formalizes the definitions of semantic space, experts/gates, RAG memory and retrieval, seam penalty, RSVP fields, blanket and free energy, and stigmergic reinforcement.

The provided text is a troubleshooting guide for managing bibliographies using LaTeX and BibTeX, specifically focusing on the plain style and natbib package for author-year citations (plainnat). Here’s a detailed explanation:

1. Style Selection: The first part of the text discusses how to choose between numeric (plain) and author-year (plainnat) citation styles in LaTeX documents. For the numeric style, you should use \bibliographystyle{plain} and ensure there is no additional natbib package loaded. If you prefer the author-year format, load the natbib package with either [numbers] (for numeric) or without any options (for author-year).

2. Troubleshooting: The text then presents several steps to troubleshoot common issues when setting up bibliographies:

   • Check .aux file: Open the .aux file generated after running xelatex or pdflatex. It should contain \bibstyle{plain} and \bibdata{yourfile}. If these lines are missing, it indicates a problem with the LaTeX document setup for bibliography processing.

   • Verify .bib file accessibility: Ensure your .bib file is in the correct directory and readable. You can test this by running a simple BibTeX on a minimal .bib file to confirm readability.

   • Handle remaining LaTeX errors: If your full document still has errors unrelated to bibliography (like math mode or Unicode issues), apply fixes such as enclosing all math expressions in $...$ or \[...\] and replacing Unicode characters with LaTeX commands or using \DeclareUnicodeCharacter. Ensure all \cite or \citep commands reference valid keys from your .bib file.

3. Applying to Your Full Document: If you’re working on a larger document (yarncrawler.tex), ensure the bibliography section is correctly set up with \bibliographystyle{plain} and \bibliography{yarncrawler}. All \citep commands should reference valid keys from yarncrawler.bib. Also, resolve any math mode or Unicode errors as shown in a corrected document example.

4. Compiling: Compile your document using the sequence xelatex, bibtex, xelatex, xelatex (or pdflatex if you’ve resolved Unicode issues).

5. Expected Output: After successful compilation, your .pdf should include a formatted bibliography listing cited references, and the BibTeX run will produce a .bbl file without errors about missing \bibdata or \bibstyle.

6. Further Assistance: If specific errors persist during compilation or BibTeX processing, the text advises sharing exact error messages, relevant sections of your LaTeX file, and confirmation that your .bib file is correctly located to help identify remaining issues. The text also offers the option of receiving a fully corrected version tailored for pdfLaTeX or XeLaTeX if needed.

In summary, this guide provides comprehensive instructions on setting up bibliographies in LaTeX using BibTeX, troubleshooting common issues, and ensuring proper formatting and compilation.

Yarncrawler semantic parser

The Yarncrawler Framework is conceptualized as a unique semantic parser that maintains a Markov blanket for coherence. Here’s a detailed summary and explanation of the key components:

1. Core Intuition: The framework views entities (organisms, systems, or agents) as self-repairing parsers. Instead of passively interpreting data, they actively re-knit their code/body plan from semantic threads encountered in their environment. This dynamic approach allows them to adapt and survive under changing constraints by continuously rewriting their own grammar and lexicon in real time.

2. Markov Blanket Maintenance: The Markov blanket is a critical structure that separates ‘self’ (internal states) from ‘world’ (external states). Yarncrawler doesn’t treat this boundary as static; instead, it maintains the blanket through a homeorhetic process—a dynamic equilibrium. This involves:

   • Sensory Nodes: These are incoming data threads parsed into provisional semantic attractors.
   • Active Nodes: Outgoing interventions woven back into the environment.
   • Internal States: Recursive source code continuously patched by the crawler itself.
   • Blanket Dynamics: Regulate entropy exchange to keep internal parsing operations coherent, preventing collapse into noise or rigidity.

3. Semantic Parsing Function: Yarncrawler’s parsing is trajectory-aware—it doesn’t treat data as static tokens but as threads with trajectories across space and time. Parsing involves tracking, bending, and re-stitching these threads into the crawler’s semantic mesh. Noise isn’t discarded; instead, it’s annotated for future interpretation in light of new context, making Yarncrawler a recursive semantic compiler where each crawl is both interpretation and partial recompilation of itself.

4. Self-Modification & Repair: Unlike conventional parsers that assume fixed rules, Yarncrawler identifies breakdowns (holes, tears, entropy leaks in the Markov blanket), repairs them by re-threading meaning into its grammar, and propagates resilience through storing trajectory memory—past paths act as scaffolds for future interpretation. This self-repair is likened to robots mending their bodies or plants/animals maintaining homeorhetic Markov blankets—they weave themselves back together in response to changes rather than merely reacting.

5. Theoretical Implications: The framework formalizes active inference in semantic terms, minimizing surprise by continuously repairing its interpretive apparatus (Free Energy Principle). Within the scalar-vector-entropy field framework, it embodies a local semantic attractor that keeps viable bounds on Φ, 𝒗, S. It also models how systems can remain semantically coherent amidst high-dimensional, noisy input streams—relevant to AI and cognition studies.

6. Summary: In essence, the Yarncrawler Framework is a model of agents that crawl semantic landscapes, parse inputs as trajectory-based threads, maintain coherence via Markov blankets, self-repair when encountering entropy breaks, and recursively weave themselves into both world and meaning—essentially parsing itself into existence.

In the given text, a field-theoretic Lagrangian formalism for molecular swarming using a Yarncrawler functor master equation is proposed. The system consists of several components: species concentrations ((c_i)), a domain (()), a membrane bounding the domain, and reaction-diffusion dynamics with semi-permeable boundary conditions (Markov blanket).

1. Reaction-diffusion dynamics within the domain are described by the diffusion equation, where (R_i()) represents bulk reactions: [ = -_i + R_i() ] The flux ((_i)) is driven by diffusion ((-D_i c_i)), where (D_i) is the diffusion coefficient, and (c_i^{}) and (c_i^{}) denote concentrations inside and outside the domain, respectively.

2. The membrane acts as a semi-permeable Markov blanket with boundary conditions: [ i |{} = P_i(c_i^{} - c_i^{}) + J^{}_i(V, , ) + J^{}_i(, ) ] Here, (P_i) is the permeability coefficient, and (J^{}_i) and (J^{}_i) represent channel-mediated electrodiffusive flux and active transport (energy-consuming), respectively. The outward normal (()) separates in/out concentrations.

3. Selective ion channels are modeled using the Nernst-Planck equation, which describes electrodiffusion through a pore of length (l): [ J^{}_i = - ( c_i + ) _i(t) ] Here, (_i) is the gating variable representing channel open probability. The gating dynamics can be described using a simplified Hodgkin-Huxley model or ligand-gated kinetics: [ _i = _i(, )(1 - _i) - _i(, )_i ] where (_i) and (_i) are activation and inactivation rate constants, respectively.

This formalism captures molecular swarming using diffusion, semi-permeable membranes (Markov blanket), selective channels/pumps, and collective autocatalysis within a field-theoretic Lagrangian framework. The system’s behavior can be studied using this master equation to analyze the dynamics and emergent properties of molecular swarms.

To complete the formal sketch as a citable LaTeX section, one would include: - Definitions for the variables and constants used (e.g., (c_i), (), etc.) - Statements of the main equations and boundary conditions - Explanation of how these components interact to model molecular swarming behavior - Discussion on the relationship between this formalism and existing work in sheaf models of cognition, active inference, and typed program synthesis/MDL.

This text presents a mathematical formulation of the Yarncrawler model, which is a theoretical framework for understanding how biological systems maintain their internal organization (i.e., their “blankets”) against external perturbations and noise. The Yarncrawler model unifies several key concepts, including:

1. Trajectory-aware semantic parsing with Markov-blanket maintenance: This refers to the idea that living systems parse or interpret their environment based on certain rules or semantics (the “parser”), while also maintaining a semi-permeable boundary (the “Markov blanket” or membrane) between their internal and external environments. In this context, “trajectory-aware” means the system’s actions are guided by its history or current state rather than fixed coordinates.

2. Reaction-electrodiffusion with semi-permeable membranes, selective channels, pumps, chemotaxis: This involves the physical processes occurring within and around a cell or similar biological compartment. It includes chemical reactions (represented by diffusion equations), electrical potentials due to ions like in neurons or other excitable cells, and various transport mechanisms like channels and pumps that selectively allow certain molecules through the membrane, following concentration gradients or electrochemical potentials. Chemotaxis refers to directed movement of cells or organelles in response to chemical signals.

3. RSVP’s (Reaction-Semantics-Voltage-Permeability) bookkeeping: This is a way of organizing and tracking the system’s key variables and processes. RSVP likely stands for:

   • Reactions: chemical transformations within the system.
   • Semantics: the parsing or interpretation of environmental cues by the biological system.
   • Voltage: electrical potential differences, often due to ion concentration gradients.
   • Permeability: how easily substances can pass through the semi-permeable membrane.

The mathematical framework is based on a Lagrangian approach with several components:

• Bulk (interior) Lagrangian: This describes the dynamics of concentrations, electric potentials, and semantic gauge fields inside the domain Ω. It includes terms for diffusion, reactions (including autocatalysis and collectively autocatalytic sets), electrostatics, and a semantic energy term to account for the system’s parsing or interpretation of its environment.

• Boundary Lagrangian: This part governs the dynamics on the boundary Γ (the semi-permeable membrane). It includes terms for channel open probabilities and pump flux intensities, which control the selective passage of substances across the membrane based on concentration gradients or electrical potentials.

The system’s behavior is derived from a variational principle, which is subject to certain constraints to enforce physical conditions (like mass conservation) and boundary conditions (like fixed concentrations at the external environment). The resulting Euler-Lagrange equations describe how the system evolves over time, capturing its intricate interplay between reactions, diffusion, electrical potentials, and semantic processing.

This mathematical framework allows for a unified treatment of diverse biological phenomena, from molecular-scale autocatalysis to cell-level homeorhesis (stable, non-equilibrium dynamics), providing a theoretical basis for understanding how living systems maintain their organization in the face of internal and external fluctuations.

The provided text describes a sophisticated model for understanding complex biological systems, particularly in the context of cellular dynamics. The model is structured around a Lagrangian density (L), which consists of several key components that collectively govern the behavior of the system. Let’s break down each part:

1. Semi-Empirical Lagrangian Density (L_sem): This term represents the core dynamics of the system, focusing on the behavior of a gauge field Aμ. Here are its components:

   • Yang-Mills term (-tr(F²)/4g²): This is a standard term in Yang-Mills theory, representing the self-interactions of the gauge field. It’s associated with the electromagnetic force in quantum physics but here serves as a general interaction term.

   • Semantic Term (κ⟨A₀, ∇A Φ{RSVP}(c, φ)⟩): This term is unique to this model and introduces a coherence potential Φ_{RSVP}, which acts as a proxy for the nonequilibrium free energy. It pulls Aμ towards minimizing this potential while ensuring smoothness (Yang-Mills plus inertial regularization).

   • Inertial Term (-η/2||D_t A_i||²): This term represents inertial effects, acting like a damping force to prevent excessive acceleration.

2. Boundary Lagrangian Density (L_bdy): This term governs the interactions at the boundary of the system, often referred to as the “Markov blanket.” It comprises several sub-terms:

   • Passive Permeation (P_i(c_i^out−c_iin)): This represents the diffusion of species across a semipermeable membrane driven by concentration gradients.

   • **Selective Channel (J^{chan}_i(Δφ,γ)):** This term models channels that allow specific ions to pass through based on conditions like voltage (Δφ) and gate state (γ). The flux here can be GHK or Nernst-Planck.

   • **Active Pump (J^{pump}_i(c,Π)):** This term represents pumps that use energy (like ATP) to move ions against their concentration gradient. Flux here depends on the chemical potentials and is often modeled using Michaelis-Menten kinetics.

   • Quadratic Terms (-1/(2σ_γ,k²)(dot(γ_k)-f_k(Δφ,ligand))² & -1/(2σ_Π,a²)(Π_a−Π_a⋆(c,ΔG_{ATP}))²): These terms penalize deviations from the specified gating and pumping kinetics of channels and pumps respectively.

   • RSVP Regularization (α_bdy Φ_{RSVP}^Γ({c_iin−c_i^out})): This term softly regularizes contrasts between interior and exterior concentrations, promoting the maintenance of viable gradients without strictly enforcing equilibrium (homeorhesis).

3. Euler-Lagrange Equations / Yarncrawler Functor Master Equation (YFME): By varying the action S over all fields and currents with natural boundary conditions, we derive the following equations:

   • Continuity + Constitutive Law: This equation describes how concentrations change over time due to reactions (R_i(c)) and diffusion/electrodiffusion (J_i = J^⋆_i − M_i(c)∇λ_i). Here, λ_i are Lagrange multipliers used to enforce the constraint of incompressibility.

   • Electrodiffusion (Poisson): This is Poisson’s equation for the electrical potential φ, describing how it changes based on charge distributions within the system.

   • Semantic Gauge Descent: This equation governs how the gauge field Aμ evolves to minimize the coherence potential Φ_{RSVP}, with the gradient of this potential transported through the connection (A). These ‘semantic repairs’ or ‘typed rewrites’ represent adjustments to maintain system coherence.

   • Boundary Flux Law: This law dictates how fluxes (J_i) interact with the boundary, ensuring that all exchanges between interior and exterior pass through designated channels and pumps. It includes dynamics for gate and pump states driven by concentration differences and ligand binding.

The model as a whole aims to capture the interplay of chemical reactions, electrical potentials, and gating/pumping mechanisms in a cellular context while maintaining system coherence through the RSVP potential. The use of a Lagrangian formulation allows for a flexible and extensible framework that can incorporate diverse biological phenomena.

This text outlines an extensive framework for modeling complex systems, particularly biological ones, using a combination of thermodynamics, information theory, and mathematical models. Here’s a detailed explanation:

1. System Encoding (S, A): The system is represented by two components - ‘S’ for species concentrations and ‘A’ for abstract variables or semantic descriptors. This pair is encoded as a boundary constraint, which could mean that the behavior of the system at its boundaries (interface with the environment) follows certain rules defined by this constraint.

2. RSVP Bookkeeping: RSVP stands for “Reaction-diffusion Stochastic Variational Principle.” It’s a free-energy principle used to steer the system towards higher coherence (lower free energy). The free energy function, Φ_RSVP(c, φ), is composed of two parts:

   • Entropy Term: This term penalizes deviations from a reference concentration c_i^ref for each species i. It’s calculated as the sum over all species i of the integral over the spatial domain (Ω) of (c_i ln(c_i/c_i^ref) - c_i + c_i^ref) dx.

   • Flux Term: This term penalizes the fluxes (ci_in - ci_out) across the boundaries (Γ). It’s calculated as β/2 sum over all species i of the integral over the boundary of (ci_in - ci_out)^2 dS, where β is a positive constant.

3. Semantic Descent & Coherence: The semantic variables A_μ (often referred to as ‘flows’) evolve to minimize the RSVP free energy, thereby increasing system coherence. Meanwhile, channels/pumps export entropy through the boundary (Γ) to keep the total entropy (S) bounded, a characteristic of non-equilibrium steady states (NESS).

4. Autocatalysis & Reaction Acceleration by Food (RAF): This section introduces autocatalytic reactions and RAF. Autocatalysis is exemplified by the reaction X + S → 2X. RAF enhances certain reactions within a closure (food set), increasing the dominant eigenvalue of the Jacobian matrix, thereby improving system repair and resilience to losses.

5. Gaussian-Blur Affordances: This concept introduces ‘smoothed gradients’ for swarm behavior, preventing brittle responses based on precise mappings. The perception scale is set by σ (sigma).

6. Rayleigh Dissipation & Master Equation: A quadratic dissipation potential is added to account for non-conservative processes like channels/pumps and semantic motions. This forms the Rayleigh dissipation function, R. The ‘Yarncrawler Functor Master Equation’ (YFME) is then derived as a damped, constrained Euler-Lagrange system that includes this dissipation function.

7. Benefits of the Framework: This framework provides several advantages:

   • Blanket Maintenance: Boundary conditions ensure stationarity, with sensors (channels/permeation) and actuators (pumps) playing their respective roles.

   • Active Parsing: Semantic variables A_μ descend along the RSVP free energy to parse information actively, guided by boundary control laws (γ, Π).

   • Self-Repair: Gauge movements (local rewrites) reduce the free energy while maintaining type/gauge constraints, enabling self-repair.

   • Homeorhesis: Steady flows, not fixed points, stabilize viability, with entropy exported through boundaries.

   • RAF vs Single-Loop: RAF enhances spectral properties of the Jacobian matrix, improving system recovery under noise or leaks compared to single-loop autocatalysis.

The text concludes by suggesting ways to implement and test this framework, including choosing a specific instantiation (number of species, reaction rates, etc.) and solving for concentrations using Poisson’s equation. The model’s performance can be tracked via metrics like blanket viability, repair rate, dominant eigenvalue, and free energy.

The model draws inspiration from active inference, Yang-Mills theories, and the GENERIC (General Equation for Non-Equilibrium Reversible-Irreversible Coupling) framework.